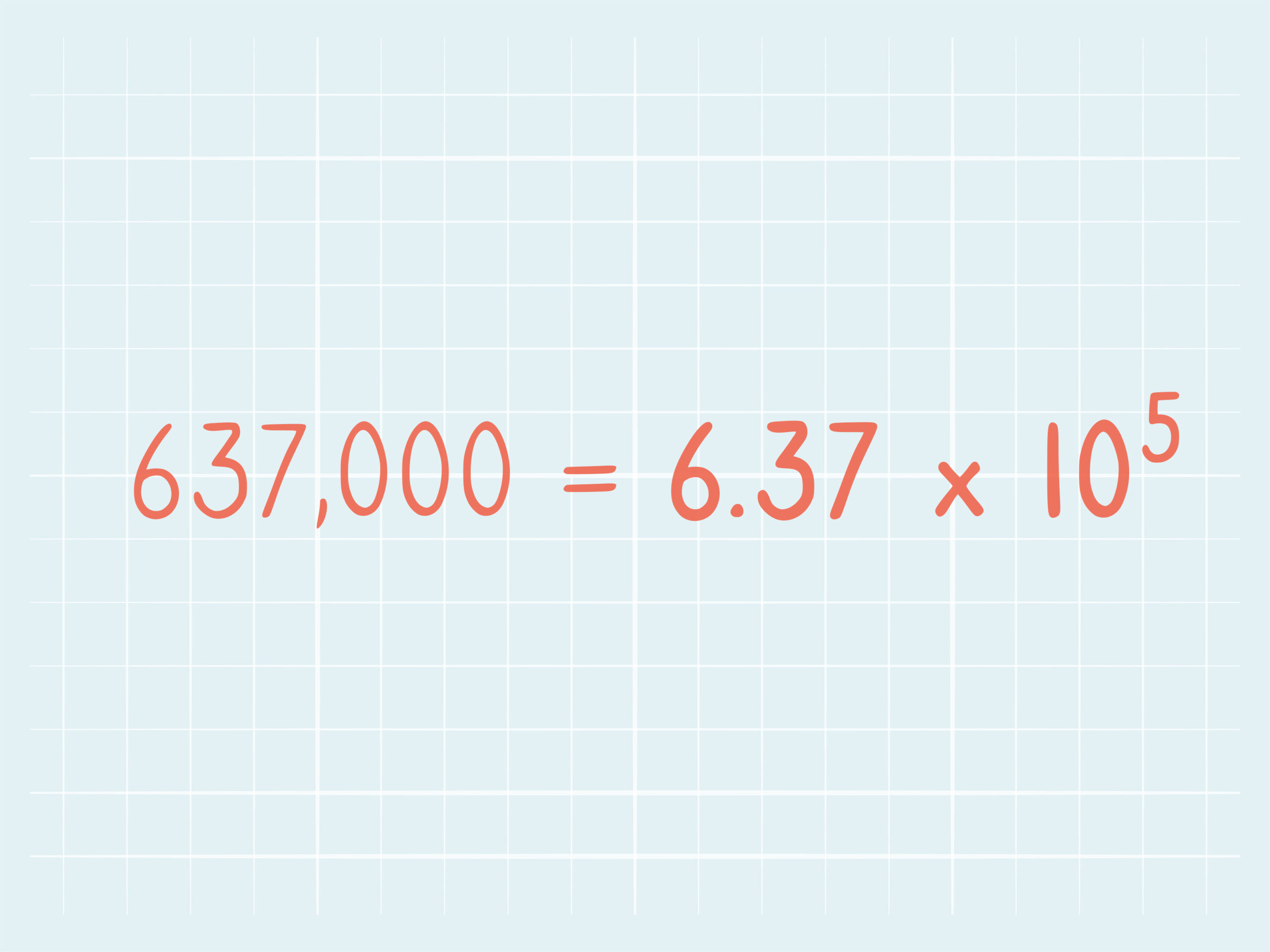How to Write Numbers in Standard Form – Standard Form is used to show the exact location of the digits in a number. The standard form of a number makes it easier to: compare one number with another, and determine which has the larger value.
Standard form is one of the most popular forms in mathematics. It is also known as prime factorization method. If you are tasked to write a number by using prime factors, this post will help you out.
The standard form is also called scientific notation in the United States, a method used to express very large and small numbers in decimal form. It is used in both science and maths as shorthand rather than using the actual number every time you use it. Standard form makes calculation much easier rather than using a number that has multiple place values. Simply try a free standard form converter online that is designed to turn any number into its standard form within a fraction of seconds.
Table of Contents
What is The Standard Form?
A way of writing small and large numbers with one number before the decimal point and multiplied by a power of 10. For Example 290000 is a number which is written in standard form as 2.9 X 105. Use an online standard form calculator that helps to convert the number in standard form and also measure the Scientific E-Notation, Engineering notation, and Real numbers of the given number.
Groups of Three:
The standard form refers to a form of notation in which digits are separated with the use of commas in groups of three. These groups of digits are known as periods. For Example: The number 321957756 is usually written in the form commas as 321,957,756. The first three numbers are called as one that appears when a number is expressed in standard form. This is even true if the first group contains just 1 or 2 digits. For example the first three digits of the number 75,236,149 would be 7, 5, and 2.
Positive and Negative Exponents:
When a number is written as scientific notation, the exponent of the number tells that the term is larger or smaller. A positive exponent indicates the large number and negative number indicates about the small number which is between 0 and 1. Examples: The speed of light is about 299,792,458 meters/second. In standard form it can be written as 3.00 X 108 m/s. (remember that round the number 299 to 300 the digit at the fourth place is larger than 4). The distance between the nucleus and electrons of the hydrogen atom is 0.00000000005291772 meters, so the standard form would be 5.29 X 10-11 meters. (In this case you don’t need to round up the value because the digit before 9 is less than 5). Instead of performing complex calculations on numbers, give a try to the standard form converter that converts the number in standard form by inserting the decimal point in the given number.
Arithmetic with Numbers in Standard Form:
Addition and Subtraction:
The addition and subtraction of numbers in standard form is easy, as long as they have the same exponents. You can simply add or subtract the strings of the digits, if numbers have different exponents, and convert one of the numbers with the exponent of the other. Example: Add the number 4.45 X 1010 and 3.75 X 108. The first number is the same number as 445 X 108. Remember that, as the decimal point moves, the exponent will change. By adding them we get 447.75 X 108or – less accurately – 448 X 1010. Try an online standard form calculator helps you to write the large and small numbers with a power of 10.
Multiplication and Division:
When multiplying the number in standard form, you just need to multiply the strings and add the exponents. When you divide the by other numbers then you ought to apply the division operation on the number and subtract the exponent. Examples
- Multiply 4.35 X 108 by 2.64 X 104.
Convert to standard form: It can be written as 11.49 X 1012.
- Divide 5.23 X 108by 1.24 X 104.
After converting to standard form the answer will be written as 4.22. X 104.
Method 1: Writing Large Numbers
- Place a decimal point and a 0 next to the last digit of a whole number. All whole numbers have an implied “.0” at the end. Rather than trying to visualize this, write it out. Place the decimal point to the right of the last digit, then add a 0 after it.[1]
- If the original number was 1,500,000, then write it was 1,500,000.0.
- If the number is already a decimal, like 1,200,000.325, skip this step. For the next step, count from the decimal point that’s already there.
- Count the place values between the decimal point and the last digit on the left. For an easy counting method, place your pencil on the decimal point. Then move it left and stop at every space between the numbers. Count each space until you reach the first digit in the number.[2]
- Since the original number is 1,500,000.0, count until you reach the 1. There are 6 place values between the decimal point and the 1.
- Remember the amount of values you counted. This is important later on.
- This also works without zeroes. For 657,799,596.0, there are 8 place values between the decimal point and the 6.
- The first few place values are ones, tens, hundreds, thousands, ten thousands, hundred thousands, and millions. The place values continue rising as numbers get bigger.
- Move the decimal point between the first and second digits on the left. Once you reach the space between the first and second digits, stop counting. Add a decimal point here and erase the original decimal point.[3]
- The number 1,500,000.0 changes to 1.500000.
- Do the same action if the second digit is a zero. For instance, 5,000,000 becomes 5.000000.
- If the decimal point was printed on the page and you can’t erase it, put a line through it so you remember it’s been moved.
- Eliminate any zeros left at the end of the number. If the number ends with 1 or more zeros, then you can ignore them. Either erase them or write the number again with the zeros omitted.
- After eliminating the extra zeros, 1.500000 becomes 1.5.
- Only get rid of zeros at the end of the number. If the number is 8.100200, only get rid of the last 2 zeros so the number is 8.1002.
- Write 10 raised to the power of the spaces between the decimal points. This is where the place values you counted are important. First write the number 10. Then add an exponent equal to the number of place values you counted between the decimal points.
- Since there are 6 place values between the decimal points in 1.5 (1,500,000), the exponent is 106.
- In standard form, the number with an exponent is always 10, never a different number.
- Express the equation as the number multiplied by 10 and its exponent. Place the number that you converted first. Then add a multiplication symbol, followed by 10 and the exponent. This represents a number in standard form.
- For the original number, 1,500,000, the standard form is 1.5 x 106.
How to Write Numbers in Standard Form
Method 2: Expressing Very Small Numbers
- Count the place values between the decimal point and the first non-zero digit. Standard form also works in the opposite direction to express very small numbers. Rather than moving right to left, move left to right. Place your pencil on the decimal point. Then count the amount of place values between the decimal and the first non-zero digit.[7]
- If the original number is 0.000325, count the place values between the decimal point and the 3. There are 4 spaces.
- There shouldn’t be zeros at the end of a decimal. If there are, erase or cross them out before counting the spaces.
- Move the decimal point to the right of the first non-zero digit. Once you’ve counted the spaces, place a decimal point after the first non-zero digit. Erase or cross out the original decimal point so your know it moved.[8]
- If the original number is 0.000325, move the decimal point and eliminate the zeros so it’s 3.25.
- If there are zeros between 2 non-zero digits, keep them. For .034002, write 3.4002.
- Write 10 raised to the power of the spaces between the decimal points. This step is the same as when you convert a large number to standard form. First write 10. Then take the number of spaces you counted between the 2 decimal points and write it as an exponent.[9]
- If the original number was 0.000325 and there are 4 spaces between the decimal points, write 104.
- Make the exponent negative. For small numbers, the exponent must be negative to indicate which direction the decimal point moved. Simply add a negative sign to the exponent to negate it.[10]
- The original exponent, 104, becomes 10-4.
- Express the equation as the number multiplied by 10 and the negative exponent. For the final step, put the equation together. Write the number first. Then add a multiplication sign and the 10 plus the negative exponent after. This expresses the number in standard form.[11]
- For the final result, 0.000325 becomes 3.25 x 10-4 in standard form.
Method 3: Converting Numbers from Written Form
- Convert each individual part of the number to numerical form. Sometimes numbers are written out, making conversion to standard form tricky. In this case, convert the number to numerical form first. Large numbers have multiple sections. Write each one out in numerical form first.[12]
- If a number is spelled out as six hundred and thirty-seven thousand, four hundred ninety-two, start at the left. The first part is six hundred and thirty-seven thousand. Write this as 637,000. The second part is four hundred, so write 400. The final part is ninety-two, so write 92.
- You can do the same with small numbers as well. Very small numbers are common in measurements, like “one-thousandth of an inch.” The thousands place value is 4 spaces to the right of the decimal point. So in written form, this is 0.0001.
- Another way to convert small numbers is to imagine them as fractions. “One-thousandth of an inch” is equal to 1/1,000. Divide 1 by 1,000 and get 0.0001.
- Add up the different parts of the number. Once you’ve expressed the different parts of the written number in numerical form, finding the numerical form for the entire number is easy. Set up an equation and add together all the parts of the number. The sum is the written number expressed in numerical form.
- For our example, your equation is 637,000 + 400 + 92. The result of the equation is 637,492.
- If you’re in the US, remember to add a comma after every 3 digits starting from the left to keep track of the number. If you end up with 545600, for example, make it 545,600.
- Outside the US, use decimal points instead of commas. So 545,600 should be 545.600.
- Go through the process to place that number in standard form. Once you express the number in numerical form, then expressing it in standard form is much easier. Simply go through the same process as you would for any other number to find its standard form.
- For 637,000, going through the process gives you 6.37 x 105.
- Do the same with small numbers as well. If one-thousandth of an inch is 0.0001, then convert it to standard form by going through the process to write small numbers. The result is 1 x 10-4.
Conclusion
Standard form is a way to write numbers in reduced form. You can easily convert a number with proper place value standard form into expanded form. The most common use of the standard form is by students to check their work. When going from expanded to standard with a number it is important not to make any mistakes.