How to Write Numbers in Scientific Notation

How to Write Numbers in Scientific Notation – Scientific notation is a convenient notation for writing very large or very small numbers. The notation has an exponent or power of ten so that the number is now always between 1 and 10, and now represented as a decimal point. Let us learn how to write big and small numbers in scientific notation steps by step, with examples.

Exponent is a mathematical operation, it represents how many times a number is multiplied by itself. It involves two numbers called base and power, power is written as a superscript of the base. it shows base is multiplied by itself power number of times. See example, 34 = 3 × 3 × 3, here the base is 3 and power is 4, so 3 is multiplied by itself 4 times. Another example, 53 = 5 × 5 × 5, here the base is 5 and power is 3, so 5 is multiplied by itself 3 times.

Table of Contents

Scientific notation

Scientific notation is useful for representing a very large or very small number skillfully. It is used for numbers in order to write numbers in standard form, also it helps in writing large numbers. In Scientific notation, a number is written as,

Attention reader! All those who say programming isn’t for kids, just haven’t met the right mentors yet. Join the  Demo Class for First Step to Coding Course, specifically designed for students of class 8 to 12. 

The students will get to learn more about the world of programming in these free classes which will definitely help them in making a wise career choice in the future.

a × 10b

  • Where a is a non-zero number lie between 1 to 10 i.e. 1 ≤ a < 10 and be negative also and b can be any number.
  • Here b+1 shows the number of digits in the given number.

How to Write Numbers in Scientific Notation

  1. Write the number as a decimal (if it isn’t one already).Suppose you want to change the number 360,000,000 to scientific notation. First, write it as a decimal:360,000,000.0
  2. Move the decimal point just enough places to change this number to a new number that’s between 1 and 10.Move the decimal point to the right or left so that only one nonzero digit comes before the decimal point. Drop any leading or trailing zeros as necessary.Using 360,000,000.0, only the 3 should come before the decimal point. So move the decimal point eight places to the left, drop the trailing zeros, and get 3.6:360,000,000.0 becomes 3.6
  3. Multiply the new number by 10 raised to the number of places you moved the decimal point in Step 2.You moved the decimal point eight places, so multiply the new number by108:3.6 x 108
  4. If you moved the decimal point to the right in Step 2, put a minus sign on the exponent.You moved the decimal point to the left, so you don’t have to take any action here. Thus, 360,000,000 in scientific notation is 3.6 x 108.

Changing a decimal to scientific notation basically follows the same process. For example, suppose you want to change the number 0.00006113 to scientific notation:

  1. Write 0.00006113 as a decimal (this step’s easy because it’s already a decimal):0.00006113
  2. To change 0.00006113 to a new number between 1 and 10, move the decimal point five places to the right and drop the leading zeros:6.113
  3. Because you moved the decimal point five places to the right, multiply the new number by 10–5:6.113 x 10–5So 0.00006113 in scientific notation is 6.113 x 10–5.

When you get used to writing numbers in scientific notation, you can do it all in one step. Here are a few examples:

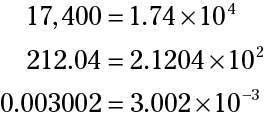
image0.jpg
a table showing how numbers are written in different formats such as in decimal form, as a power of 10, and in scientific notation. for example, one millionth is written in decimal form as 0.000001, 10^-6 when written as a power of 10 then in scientific notation as 1×10^-6. on the other hand, one thousand is written as 1,000 in decimal form, 10^3 as a power of 10, and written in scientific notation as 1×10^3.

How to Change Numbers Into and Out of Scientific Notation

Method 1: Converting Numbers Into Scientific Notation

  1. Start with a very small or very large number. You’ll need to start with a very small or a very large number if you want to successfully convert it into scientific notation. For example, 10,090,250,000,000 is very large; 0.00004205 is very small.[1]
  2. Cross out the original number’s decimal point. This is the first step to beginning to convert the number into scientific notation. If you’re working with the number 0.00004205, just write an “x” over the decimal point.
  3. Add a new decimal point to the number so that there’s only one non-zero digit in front of it. In this case, the first non-zero number is 4, so place the decimal point after the 4 so that the new number reads 000004.205.[3]
    • This works for large numbers, too. For example, 10,090,250,000,000 would become 1.0090250000000.
  4. Rewrite this number to drop any insignificant digits. Insignificant digits are any zeros that are not in between other, non-zero digits.[4]
    • For example, in the number 1.0090250000000, the zeroes at the end are insignificant, but the zeros between the 1 and then 9, and between the 9 and the 2, are significant. Rewrite this number as 1.009025.
    • In the number 000004.205, the leading zeros are insignificant. Rewrite this number as 4.205.
  5. Write “x 10” after the rewritten number. Just write 4.205 x 10 for now.[5]
  6. Count how many times you moved the original decimal point. In the case of 0.00004205 to 4.205, you moved the decimal point over 5 times. In the case of 10,090,250,000,000 to 1.0090250000000, you moved the decimal point 13 times.[6]
  7. Write that number as the exponent over the number 10. For 1.0090250000000, write x 1013. For 4.25, write x 105.[7]
  8. Decide if the exponent should be negative or positive. If your original number was very large, the exponent should be positive. If your original number was very small, the exponent should be negative.
    • For example: the very large number 10,090,250,000,000 becomes 1.009025 x 10 13 while the very small number 0.00004205 becomes 4.205 x 10-5.
  9. Round your number as much as necessary. This depends on how certain you need to be in your answer. For example, 1.009025 x 1013 might be better off as 1.009 x 1013 or even as 1.01 x 1013, depending on how accurate you need to be.

Method 2: Converting Numbers from Scientific Notation

  1. Decide if you will be moving the decimal point to the left or to the right. If the exponent on the “x 10” part of the number is positive, then you will be moving the decimal places to the right; if the exponent is negative, you will be moving the decimal places to the left.[8]
  2. Write down how many places you would need to move the decimal. In the case of the number 5.2081 x 1012, you will be moving the decimal point over five spaces to the right. If the exponent is a -7, you move left seven places; if the exponent is a 5, move right five places.[9]
  3. Move the decimal point over, adding zeroes for every empty space. You may have to add them in front of or behind the number, depending on whether you are moving left or right. If you’re moving the decimal point over 12 spaces to the right from the number 5.2081, then the new number becomes 5208100000000.[10]
  4. Write the new decimal point after you’ve moved over the correct amount of spaces.
  5. Add commas to any number over 999. Go through the digits, from right to left, putting a comma in front of every group of three digits. For example, 5208100000000 becomes 5,208,100,000,000.

Examples of How to Write Decimal Numbers into Scientific Notation

Example 1: Rewrite the given decimal number 5,800 in scientific notation.

We start by identifying where the original location of the decimal point, and its new location.

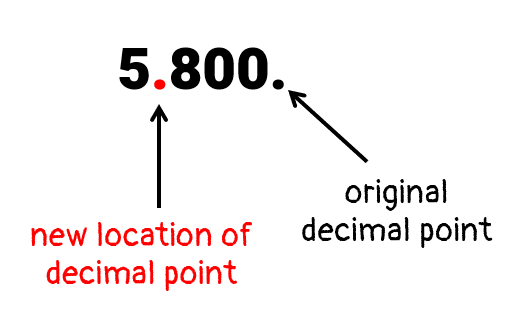
for the number 5,800, the original decimal point is located on the rightmost side of the number while the new location of the decimal point will be between the numbers 5 and 8.

Now, we move the decimal point from the starting point to its final destination while counting the number of decimal places.

  • Remember the rule above, if the decimal is moved towards the left, the count for the exponent of base 10 is positive.
from the original location of the decimal in the number 5800, we will count and move 3 decimal places to the left to get a decimal between 1 and 10, which will give us 5.800.

That makes our value of “cc” as c = 5.8c=5.8, and the power of 10 is 103. Putting them together in the required format, our final answer is

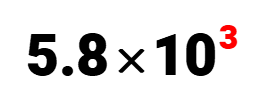
we write the number 5,800 in scientific notation as 5.8 × 10^3. note that our exponent is positive 3 because we moved 3 decimal spaces to the left.

Always remember to make sure that “cc” value always has the decimal point right after the first digit which is the case here. Great!

Example 2: Rewrite the given decimal number 1,730,000 in scientific notation.

Begin by locating the initial decimal point, and where it is going.

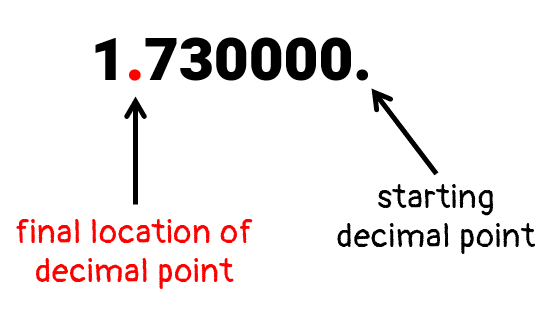
in our decimal number 1,730,000, the starting decimal point is located on the right of the last 0 which is the rightmost side of the number. when moved to get a decimal number between 1 and 10, the final location of the decimal point is between 1 and 7.

It appears that we are going to move the decimal to the left. Remember, such type of movement will incur a positive exponent for the base 10.

from its original location at the end of the number 1730000, we will move the decimal 6 places to the left which will give us 1.730000. as we move the decimal or dot to get a decimal that is between 1 and 10, we need to pay attention and count the number of decimal places we moved the decimal from.

The coefficient or “cc” value is c = 1.73c=1.73 and the power of 10 is 106. This should give us the final answer of

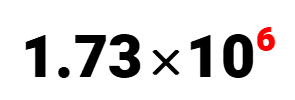
the decimal number 1730000, when written in scientific notation, is 1.73 × 10^6.

Example 3: Rewrite the given decimal number 33,335,000,000,000 in scientific notation.

The starting decimal point is on the far right. We need to move it to the left until we have a decimal number between 1 and 10.

the original location of the decimal point in the number 33,335,000,000,000 is after the last zero. to get a "c" or number between 1 and 10, we need to move the decimal point to the left ending between the first and second 3.

Moving the decimal from right to left implies that the power of 10 will have a positive integer.

we will move the decimal point 13 decimal places to the left to get a decimal number that is between 1 and 10. remember to count the number of decimal places we moved the decimal point from, which in this case is 13 places, because we need this when writing our scientific notation.

The value of the coefficient is c = 3.3335c=3.3335, and the power of 10 becomes 1013. Therefore, the final answer of our scientific notation is just

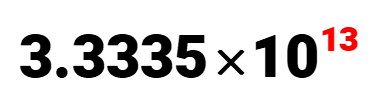
the scientific form of the number, 33,335,000,000,000 is 3.3335 × 10^13.

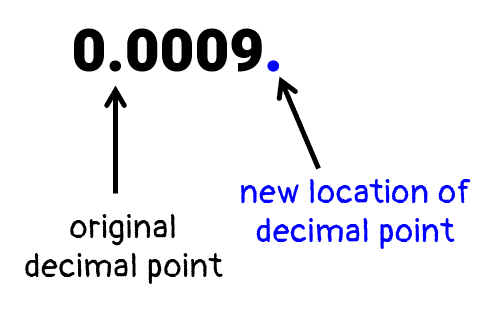
Example 4: Rewrite the given decimal number 0.0009 in scientific notation.

It is obvious that the original decimal point is to the left of the nonzero digit. We will move the decimal going to the right. The rule above states that

  • When the decimal is moved towards the right, the count for the exponent of base 10 should be negative.
in the decimal number 0.0009, the original decimal point is located between the first and second zeros. to get a number between 1 and 10, we need to move the decimal point to the right which in this case, will be located to the right side of 9 or the rightmost side of our number. from 0.0009, it will become 00009.

Moving the decimal point to the right should yield a negative exponent for the base 10.

we will move the decimal point 4 decimal places to the right to get a "c" or number between 1 and 10.

The value for cc is just c = 9c=9, and the power of 10 is 10–4. Our final scientific notation answer should be

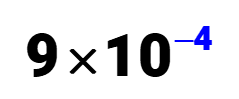
we write the decimal number 0.0009 in scientific notation as 9 × 10^-4.

Example 5: Rewrite the given decimal number 0.00000000086 in scientific notation.https://d6dec3d8283f1bb7e14b83df7a95f7f6.safeframe.googlesyndication.com/safeframe/1-0-38/html/container.html

Maybe you can predict that since the given decimal number is between 0 and 1, we should have a scientific notation with a negative power. First, identify the initial decimal point and where it is going.

in our decimal number 0.00000000086, the location of the original decimal is after the first zero. since we want to get a number from 1 to 10, we need to move the decimal point to the right ending next to the number 8. this will be the new location of our decimal point.

Let’s go ahead and move the original decimal point towards the right until the decimal point is to the right of the first nonzero digit which is 8. Going to the right means we are going to accumulate negative counts for the power of 10.

moving 10 decimal places to the right, we'll have 00000000008.6. to continue writing in scientific notation, we will drop the zeros and leave the nonzero numbers.

This gives us the coefficient value of c = 8.6c=8.6, and the power of 10 value is 10–10. Writing the final scientific notation, we have

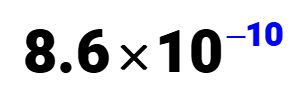
the scientific notation form of the decimal number 0.00000000086 is 8.6 × 10^-10.

Example 6: Rewrite the given decimal number 0.000000000001234 in scientific notation.

The given decimal number is less than 1, so we expect to move the decimal point towards the right such that it stops after the first nonzero digit.

we first determine the location of our original decimal point. in our given decimal number, 0.000000000001234, the original decimal is located after the first 0. we will then move the decimal point to the right to obtain a number from 1 to 10. thus, we'll have 0000000000001.234 where the new location of our decimal number is next to 1.

Let’s move the decimal point to the right, and it should accumulate a negative power of 10.

to get a decimal number between 1 and 10, we will move the decimal point 12 decimal places to the right from its original location.

We have a coefficient value of c = 1.234c=1.234, and base ten value of 10–12. This gives us a scientific notation of

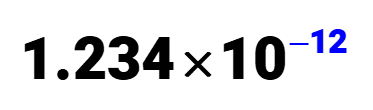
our decimal number, 0.000000000001234, can be written in scientific notation as 1.234 × 10^-12. note that we have an exponent of -12 for our base 10. that is because we moved our decimal point 12 decimal places to the right which means our exponent will be negative.

Conclusion

You are forgiven if you are slightly intimidated by scientific notation. The discipline is full of grand concepts, formidable ideas, and sometimes perplexing rules to determine the form of numbers that are expressed in scientific notation.

0 0 votes
Article Rating
Subscribe
Notify of
guest
0 Comments
Oldest
Newest Most Voted
Inline Feedbacks
View all comments
0
Would love your thoughts, please comment.x
()
x