How to Write Numbers in Expanded Form

Writing numbers in expanded form is a great way to review and learn how to find the prime factors of a number. In this article, I am going to go through the process of writing numbers in expanded form using number sentences.

Expanded form is also known as “expand these numbers” “write in expanded form”. This method of recording numbers is frequently used in mathematical dictation. Below are all the rules about how to write numbers in expanded form.

Table of Contents

Expanded Form of Numbers

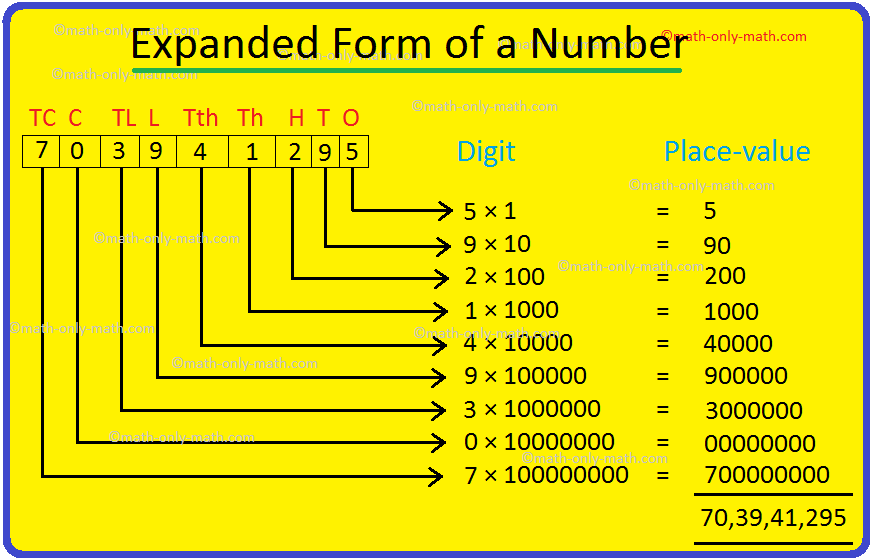
The expanded form of the numbers helps to determine the place value of each digit in the given number. It means that the expansion of numbers is based on the place value. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form. For example, the expanded form of the number 1572 is 1000+500+70+2.

Some of the examples of the expanded form of numbers are provided in the tabular form:

Number	Ten thousand	Thousands	Hundreds	Tens	Ones
723			7	2	3
1243		1	2	4	3
5679		5	6	7	9
23456	2	3	4	5	6

Let us take the number 723. In number 723, there are 7 hundreds, 2 tens and 3 ones.

More Examples on Expanded Form:

The expanded form of 90 is 90+0. In the number 90, there are 9 tens and zero ones.
300 in the expanded form is 300+0+0, as there are zero tens and zero ones.
The expanded form of 10,000 is 10000+0+0+0+0. In the number 10,000, there are zero thousand, zero hundred, zero tens and zero ones.

How to Write Numbers in Expanded Form?

Go through the below steps to write the numbers in expanded form:

Step 1: Get the standard form of the number.

Step 2: Identify the place value of the given number using the place value chart.

Step 3: Multiply the given digit by its place value and represent the number in the form of (digit × place value).

Step 4: Finally, represent all the numbers as the sum of (digit × place value) form, which is the expanded form of the number.

Example:

What is 35713 in expanded form?

Solution:

Step 1: The standard form of the number is 35713.

Step 2: The place value of the given number is:

3 – Ten thousand

5 – Thousands

7 – Hundreds

1 – Tens

3 – Ones

Step 3: Multiply the given number by its place value.

(i.e.,) 3×10, 000, 5×1000, 7×100, 1×10, 3×1

Step 4: Expanded form is 30,000+ 5000+700+10+3

Finally, the expanded form of the number 35713 is 30,000+ 5000+700+10+3.

Expanded Form of Decimal Numbers

The decimal numbers can also be written in the expanded form. While writing the decimals in the expanded form, we need to multiply each decimal digit with the increasing exponent values of 1/10. Using the place value chart, the digits after the decimal points are represented as tenth (1/10), hundredth (1/100), thousandth (1/1000) and so on.

Now, let us consider the example 83.34.

First, write the expanded form for the number before the decimal point. (i.e.) 83

The expanded form of 83 is 80+3.

Now, the expanded form 34 is written as 3(1/10) + 4(1/100) [As 3 represents the tenth position and 4 represents the hundredth position]

Thus, the expanded form of 83.34 is written as 80+3+(3/10)+(4/100)

The above-expanded form can also be represented as 80+3+0.3+0.04.

Expanded Factor Form

In expanded factor form, the standard form of the number is written in its expanded factor form. If the number is written as the sum of the product of digit and its place value, then it is called expanded factor form.

Expanded Factor Form = Sum of (Digit × Place value)

Expanded Exponential Form

In expanded exponential form, the place value of the digits is represented in terms of the powers of 10. It means that one’s place is represented by 10⁰, tens place is represented by 10¹, hundreds place is represented by 10², and so on.

For example, the expanded exponential form of 2325 is represented by:

2 – Thousands (2 ×10³)

3 – Hundreds (3 × 10²)

2 – Tens (2 × 10¹)

5 – Ones (5 × 10⁰)

Thus, the expanded exponential form of 2325 is (2 ×10³)+(3 × 10²)+ (2 × 10¹)+ (5 × 10⁰)

Part 1: Part One: Change Standard Form to Expanded Form

Look at the number in standard form. Read the number and look at how many digits are in it.^[1]
- Example: Write 5,827 in expanded form.
  - Read the number silently or out loud: five thousand, eight hundred twenty seven.
  - Notice that there are four separate digits in this number. As a result, there will be four separate places in the expanded form of this number.
Separate the digits. Rewrite the number so that each of its digits are separated by a plus sign. Leave a little room in between each digit and the plus sign that follows it. More information will need to be included there.
- Example: The number 5,827 temporarily becomes:
  - 5 + 8 + 2 + 7
Identify each place value name. Each digit in your original number corresponds to a specific place value. Starting from the lowest digit, label each digit with its appropriate place value name.^[2]
- Example: Since there are four digits in this number, you will need to count up four place values.
  - The smallest digit is 7, and that corresponds to the ones (1) place.
  - The next digit is 2, which corresponds to the tens (10) place.
  - The third digit is 8, which sits in the hundreds (100) place.
  - The fourth and final digit is 5, and it sits in the thousands (1000) place.
Multiply each digit by its appropriate place value. Multiply each separate digit in your original number by the place value that matches where it belongs within the full, original number.^[3]
- Example: [5 * 1000] + [8 * 100] + [2 * 10] + [7 * 1]
Write your final answer. Once the digits have been multiplied together, you should have the final expanded form of the original number.^[4]
- Example: The expanded form of 5,827 is:
  - 5000 + 800 + 20 + 7Advertisement

Part 2: Part Two: Change Written Form to Expanded Form

Look at the number in written form. Read the number as it is written. When a number is in this form, you should be able to identify the full value of each separate digit.^[5]
- Example: Write the following in expanded form: seven thousand two hundred eighty nine.
Identify each place value name. Write each digit separately, attaching the appropriate place value name after it. The correct place value will simply be the one that is already written beside the value. Include plus signs in between each written value.^[6]
- Note that the “tens” and “ones” place values are not specifically labeled, but they should be understood. You can indicate your understanding by marking the place value name in parentheses, but doing so is not strictly necessary.
- Example: The number seven thousand two hundred eighty nine becomes:
  - seven thousand + two hundred + eighty (tens) + nine (ones)
  - OR
  - seven thousand + two hundred + eighty + nine
Rewrite the written place value as a numeric place value. Look at each separate value. Rewrite each value as it reads to the equal numeric value.
- Example: Seven thousand + two hundred + eighty + nine:
  - Seven thousand = 7000
  - Two hundred = 200
  - Eighty = 80
  - Nine = 9
Write the final answer. You should have all the information you need now to write the original written form number in expanded form.
- Example: The expanded form of seven thousand two hundred eighty nine is:
  - 7000 + 200 + 80 + 9Advertisement

Part 3: Part Three: Expanded Form with Decimals

Look at the number in standard form. Read the number and count how many digits are in it, paying special attention to the digits that come after (to the right of) the decimal point.^[7]
- Example: Write 531.94 in expanded form.
- Read the number: five hundred thirty one and 94 hundredths.
- Notice that there are three digits before the decimal point and two digits after the decimal point. There will be a total of five separate places in the expanded form of this number.
Separate the digits. Rewrite the number, separating each individual digit by a plus sign. For now, write the decimal point, too.^[8]
- Note that the decimal point will eventually be removed, but you should keep it in place for now to prevent confusion while solving the problem.
- Leave some space in between the digits and the plus signs. More information will need to be written there.
- Example: The number 531.94 temporarily becomes:
  - 5 + 3 + 1 + . + 9 + 4
Identify each place value name. Label each digit with the place value name that matches its position in the original number.^[9]
- When working before (to the left of) the decimal point, work from the lowest number to the highest.
- When working after (to the right of) the decimal point, work from the highest number to the lowest.
- Example: You will need to count three places to the left and two places to the right.
  - For the left values:
  - The smallest number is 1, which matches the ones (1) place.
  - The second number is 3, which matches the tens (10) place.
  - The largest number is 5, which sits in the hundreds (100) place.
  - For the right values:
  - The largest number is 9, which sits in the tenths (10) place.
  - The smallest number is 4, which sits in the hundredths (100) place.
Multiply the left digits by the appropriate value. All of the digits on the left side of the decimal point must be multiplied by their matching place value. Do that now.^[10]
- Example: [5 * 100] + [3 * 10] + [1 * 1] = 500 + 30 + 1
Divide the right digits by the appropriate value. All of the digits on the right side of the decimal point must be divided by their matching place value. Do that now.
- Example: [9 / 10] + [4 / 100] = 0.9 + 0.04
Write your final answer. Combine all of your rewritten values together, placing plus signs in between each one. Remove the decimal point. This will be your final answer.^[11]
- Example: The expanded form of 531.94 is:
  - 500 + 30 + 1 + 0.9 + 0.04Advertisement

Part 4: Add Expanded Form

Look at the problem. Verify that you need to add together the expanded forms of two or more numbers. If the problem is written out in both words and numerals instead of numerals only, pull the numerals out of the problem and set them up in the addition format.^[12]
- If you are given numbers in written form or standard form but need to show your work in expanded form, rewrite each number in expanded form before continuing.
- Example: Add [500 + 30 + 6] and [80 + 2] together.
  - Rewrite the problem as: 500 + 30 + 6 + 80 + 2
Separate the numbers by place value. Identify all numbers in the ones place value, followed by all numbers in the tens place value, followed by all the numbers in the hundreds place value. Continue in this manner to identify all currently used place values. Rewrite the problem, arranging the various place values together.^[13]
- Example: For 500 + 30 + 6 + 80 + 2:
  - Hundreds place value: 500
  - Tens place value: 30 + 80
  - Ones place value: 6 + 2
Add each place value group separately. Add up all of numbers in each place value category. Start with the ones place value and work your way up to the largest place value.^[14]
- Note that if the sum of one place value exceeds the proper amount of digits within that place value category, you must add the extra digit to the place category above it.
- Example: Start with the ones place value, followed by the tens, followed by the hundreds.
  - 6 + 2 = 8
  - 30 + 80 = 110; since this value exceeds the tens place category, you separate it into 100 + 10; keep the 10 here and add the 100 to the next place category as follows
  - 500 + 100 = 600
Write your final answer. Arrange the sums of each category in a row, separating them with plus signs. This is the expanded form of your answer.
- If you wanted to write the standard form of the answer, all you would need to do is add the digits together.
- Example: 500 + 30 + 6 + 80 + 2 = 600 + 10 + 8
  - In standard form, the answer would be 618.Advertisement

Part 5: Part Five: Subtract Expanded Form

Look at the problem. Make sure that you are being told to subtract the expanded forms of two numbers. If the question is phrased as a word problem, pull the numerals out of the problem and arrange them in subtraction format.
- Note that you should rewrite any numbers originally in standard or written form if the question explicitly tells you to show your work in expanded form.
- Example: Subtract [500 + 70 + 1] from [800 + 10 + 4].
  - Rewrite as: [800 + 10 + 4] – [500 + 70 + 1]
  - Or: 800 + 10 + 4 – 500 – 70 – 1
Separate the numbers by place value. Identify all numbers falling into separate place value categories (ones, tens, hundreds, thousands, etc.). Rewrite the problem so that all numbers belonging to the same place value category are grouped together.^[16]
- Example: For [800 + 10 + 4] – [500 + 70 + 1]:
  - Hundreds: 800 – 500
  - Tens: 10 – 70
  - Ones: 4 – 1
Subtract each place value group separately. Subtract the numbers in each place value category. Start with the lowest category (ones) and gradually work your way up to the highest.^[17]
- If the number you are subtracting from is smaller than the number you must subtract from it, you will need to take an entire place value from the category above it. For instance, take “10” from the tens category if the values in the ones category cannot be subtracted as they are.
- Example: Start with the ones category, followed by the tens, followed by the hundreds.
  - 4 – 1 = 3
  - 10 – 70; since “70” is larger than “10,” you’ll need to take “100” from the “800” and add it to the “10,” making this equation: 110 – 70 = 40
  - 700 – 500 = 200; the “800” became “700” when you took the “100” for the tens category
Write the final answer. Arrange the differences from each category in a row, separating them with plus signs. This is the expanded form of your final answer.
- To find the standard form of this answer, all you need to do is add the digits of the expanded form together.
- Example: [800 + 10 + 4] – [500 + 70 + 1] = 200 + 40 + 3
  - In standard form, the answer would be: 243

Example Problem 1: Writing Numbers in Expanded Form:

Write the number 539 in expanded form.

Starting with the right-most digit, we see that there are 9 ones, 3 tens, and 5 hundreds represented by this number. Therefore we can write this in expanded form by summing each place value:

539=500+30+9539=500+30+9

Notice that each successive digit to the left of the right-most digit increases by an order of magnitude, which means that there is an additional zero added to the end of each successive number.

Example Problem 2: Writing Numbers in Expanded Form:

Write the number 1,234,567 in expanded form.

Starting with the right-most digit, we see that there are 7 ones, 6 tens, 5 hundreds, 4 thousands, 3 ten-thousands, 2 hundred-thousands, and 1 million represented by this number. The expanded form is:

1,234,567=1000000+200000+30000+4000+500+60+7

Conclusion

Expanded form is a method of writing and reading numbers and it can be accessed by everyone. It’s used in most high schools’ mathematics lessons and in many cases when reading numbers off of calculators. It is also used when reading numbers that display on digital devices such as tablets or phones where numbers are not in their short form.

0 0 votes

Article Rating