How to Write Linear Equations

Congratulations! If you landed on this page, it probably means you have a test tomorrow in math class. But don’t worry—all is not lost! In English class, you write everything from details of your most intimate family history to your personal opinions on controversial political issues. In Math class, you’re allowed to do the same thing—just with numbers. This article will enable you to learn everything about Linear Equations.

Solving linear equations is a skill that every high school student must know, but some students have a hard time understanding them. If you need some guidance on how to solve a linear equation, these examples of solving a linear equation will help you.

Table of Contents

How to Write Linear Equations

Note that the standard form of a linear equation is:

y = mx + b

Where m = slope and b = y-intercept.

Calculate the slope of the line. The slope can be found by selecting two points on the line, determining the vertical rise and the horizontal run between the points and dividing them. For example, if (3,4) and (5,6) are on the line, the slope between them would be (5 – 3) / (6 – 4), simplified to (2) / (2), simplified to 1. Include negative values, since slopes can be positive or negative.

Determine or calculate the y-intercept of the line. The y-intercept is the y-coordinate of the point where the line passes through the y-axis of the coordinate plane. For example, if the point of intersection with the y-axis is (0,5), the y-intercept would be 5. The y-intercept can be found by physically locating it on the graph or by locating the given point on the line that has an x-coordinate of 0. That point is the point of intersection. The y-intercept will be positive if it intersects the y-axis above the x-axis or negative if it intersects below the x-axis.

Write the equation y = mx + b, substituting the values for m and b you calculated or determined. The m will be your slope, and the b will be your y-intercept. Leave the y and x variables in the equation as letter variables. Include the sign of the numbers you plug in. For example, if I discovered my slope to be -3 and my y-intercept to be 5, my linear equation would be y = -3x + 5. The linear equation is complete and correctly written when the (m) and (b) are properly incorporated into the equation.

Method 1 Starting with the Variables on Opposite Sides

Look at your problem. A simple linear equation might look like $7x-10=3x-6$ .
Check the equation for varying terms and constant terms. Varying terms are numbers like , , or , where the number changes depending on what you plug into the variable, or letter. Constant terms are numbers like , or , where the number never changes.
- Usually, equations won’t come with varying terms and constant terms lined up on separate sides. In the example above, the left-hand side (LHS) has both varying and constant terms, as does the right-hand side (RHS).
Prepare to move the numbers around so that the varying terms are on one side and the constant terms are on the side such as in 16x−5x=32−10 (that equation is solved in example 2). In order to do this, you may have to subtract or add the numbers you want to move from both sides. In the next step, you’ll see how to do that in example 1.
- The equation $16x-5x=32-10$ does have all the varying terms on one side (LHS), while all the constant terms are on the other side (RHS).
Move the varying terms to one side of the equation. It doesn’t matter to which side you move the varying terms.
- In example 1, $7x-10=3x-6$ can be rearranged by choosing to subtract either $7x$ or $3x$ from both sides. Choosing to subtract $7x$ , you have:
  
  ${\begin{aligned}(7x-7x)-10&=(3x-7x)-6\\-10&=-4x-6\end{aligned}}$
Bring all the constant terms onto the other side of the equation. That is: move the constant terms so that they are on the opposite side of the equation from where the varying terms are.
- We see that

${\begin{aligned}-10-(-6)&=-4x-6-(-6)\\-4&=-4x\end{aligned}}$

Divide both sides by the coefficient of x{\displaystyle x}. The coefficient of (or , or , or any letter) is the number in front of the varying term.
- The coefficient of $x$ in $-4x$ is $-4$ . So divide both sides by $-4$ to get the value of $x=1$ .
- Our answer to the equation $7x-10=3x-6$ is $x=1$ . You can check this answer by plugging $1$ back into every $x$ variable and seeing if both sides of the equation equal the same number:
  ${\begin{aligned}7(1)-10&=3(1)-6\\-3&=-3\end{aligned}}$

Method 2 Starting with the Variables on One Side

Know that sometimes the varying terms and the constant terms will be separate. Sometimes, half of your work will be done for you. You’ll have all the varying terms on one side and all the constant terms on the other side. If this is the case, all you have to do is the following.
Simplify both sides. For the equation $16x-5x=32-10$ , we just have to subtract the numbers from one another.
3 Next, divide both sides by the coefficient of x. Remember that the coefficient of x is the number in front of the varying term.
- In this example, the coefficient of $x$ in $11x$ is $11$ . That division is $11x/11=22/11$ to get $x=2$ . The answer to the equation $16x-5x=32-10$ is $x=2$ .

Different Forms

There are many ways of writing linear equations, but they usually have constants (like “2” or “c”) and must have simple variables (like “x” or “y”).

Examples: These are linear equations:

But the variables (like “x” or “y”) in Linear Equations do NOT have:

Exponents (like the 2 in x²)
Square roots, cube roots, etc

Examples: These are NOT linear equations:

Slope-Intercept Form

The most common form is the slope-intercept equation of a straight line:

Example: y = 2x + 1

Slope: m = 2
Intercept: b = 1

Play With It ! You can see the effect of different values of m and b at Explore the Straight Line Graph

Point-Slope Form

Another common one is the Point-Slope Form of the equation of a straight line:

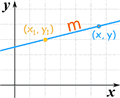Example: y − 3 = (¼)(x − 2)

It is in the form y − y₁ = m(x − x₁) where:

y₁ = 3
m = ¼
x₁ = 2

General Form

And there is also the General Form of the equation of a straight line:

Ax + By + C = 0

(A and B cannot both be 0)

Example: 3x + 2y − 4 = 0

It is in the form Ax + By + C = 0 where:

A = 3
B = 2
C = −4

There are other, less common forms as well.

As a Function

Sometimes a linear equation is written as a function, with f(x) instead of y:

y = 2x − 3

f(x) = 2x − 3

These are the same!

And functions are not always written using f(x):

y = 2x − 3

w(u) = 2u − 3

h(z) = 2z − 3

These are also the same!

The Identity Function

There is a special linear function called the “Identity Function”:

f(x) = x

And here is its graph:

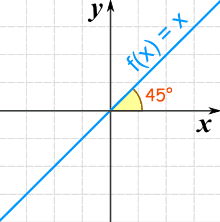
It makes a 45° (its slope is 1)

It is called “Identity” because what comes out is identical to what goes in:

In	Out
0	0
5	5
−2	−2
…etc	…etc

Constant Functions

Another special type of linear function is the Constant Function … it is a horizontal line:

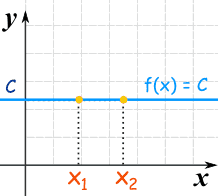
f(x) = C

No matter what value of “x”, f(x) is always equal to some constant value.

Conclusion

Linear equations can be solved graphically as well as mathematically. For those who may be unsure, there is a difference between the two approaches. Mathematically means using math. Graphically means getting your hands dirty and scribbling across a piece of paper until you see the answer you are looking for or have an idea for an answer. You can also use graphs to help you unravel further questions about what you are actually plotting onto your page.

0 0 votes

Article Rating

		y = 3x − 6
		y − 2 = 3(x + 1)
		y + 2x − 2 = 0
		5x = 6
		y/2 = 3

		y² − 2 = 0
		3√x − y = 6
		x³/2 = 16