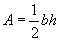How to Solve Geometry Problems – In these lessons, we look at geometry word problems, which involves geometric figures and angles described in words. You would need to be familiar with the formulas in geometry.
Key Terms
o Point
o Line
o Line segment
o Ray
o Angle
o Rectangle
o Perimeter
o Area
o Square
o Triangle
Objectives
o Get familiar with some fundamental geometric figures
o Calculate the perimeter and area of a rectangle
o Derive a formula for the area of a triangle
Geometry studies points, lines, shapes, angles, and the relationships between them. We will consider some simple shapes, such as triangles and rectangles, and will discuss how to calculate some of their properties.
Elements of Geometry
Before considering some more complicated figures, we must have an understanding of certain terms that are used throughout the study of geometry. Several fundamental geometric concepts include points, lines, and angles. A point is essentially a location-it is often represented using a small dot, and it represents a location in space and has no length, width, or depth. Several points are shown below.

A line in geometry is has most of the same characteristics as it does in real life (and in algebra). A geometric line is straight, and it extends indefinitely in opposite directions. If two lines meet at a point, then they are said to intersect. An example of a line is shown below; note that the ends of the line have arrows that indicate the line continues indefinitely.

A finite portion of a line is called a line segment. Line segments have lengths that are finite (limited) numbers, unlike lines, whose lengths are infinite (unlimited). A line segment is shown below; the ends of the line segment are shown as points.

A ray is a portion of a line with only one end point, as shown below. Its length is still infinite, but it has one identifiable end.

When two lines, line segments, rays, or some combination thereof intersect, they form an angle. An example of an angle is shown below.
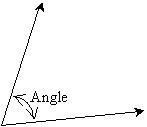
Angles can be measured in degrees (°), which range from 0° to 360°. Some example angle measures are shown below.
Using these basic geometric terms and figures, we can now turn to studying some more complicated figures.
Rectangles
A rectangle is a specific kind of closed geometric figure with four sides; an example of a rectangle is shown below.

Rectangles can be described by their two dimensions: a length (which we can call l) and a width (which we can call w). Opposite sides of a rectangle are equal in length, and the “interior” angles are all 90° in measure; thus, we can draw the rectangle as shown below.
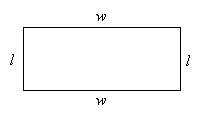
One characteristic of rectangles that we can readily calculate is its perimeter, which is the sum of the lengths of all the sides. The perimeter P is the following:
P = l + w + l + w
We can simplify this expression by converting addition of like terms into multiplication:
P = l + l + w + w
P =2l + 2w
For instance, consider the rectangle below.

Because opposite sides are equal in length, the rectangle has two sides of length 6 units and two sides of length 3 units. The perimeter is thus the following:
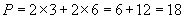
Interested in learning more? Why not take an online Pre-Algebra course?
The perimeter is 18 units. (Note that the “unit” can be inches, feet, meters, or any other type of length measurement. If the unit is specified, use that particular unit; otherwise, the generic term “units” is sufficient.)
Practice Problem: Calculate the perimeter of the rectangle below. All measurements are in feet.
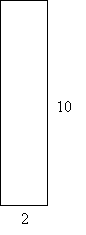
Solution: Recall that opposite sides of a rectangle are equal in length. Thus, this rectangle has two sides of length 10 feet and two sides of length 2 feet. The perimeter P is then the following:
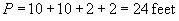
Alternatively, we could have simply used the formula we derived above.
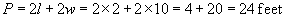
Practice Problem: A certain rectangle has a perimeter of 50 meters and a length of 14 meters. What is its width?
Solution: We can solve this problem by carefully considering the information presented and by applying what we know about solving equations. We know, first of all, that the perimeter P of a rectangle obeys the following formula, where l is the length and w is the width.
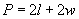
The problem statement tells us what the perimeter (P) is, as well as what the length (l) is. Let’s enter these values into the equation above and then simplify the result as best we can.
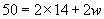
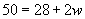
To find the width of the rectangle, we need only solve for w using the same approach that we used when solving linear equations.
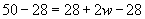
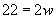
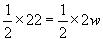
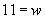
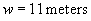
Thus, the width of the rectangle is 11 meters. Let’s check this result to be sure it works. We know from the problem statement that the length of the rectangle is 14 meters.
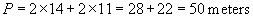
Thus, the answer checks out.
We can also calculate the area of a rectangle, which is a measure of how much space it occupies. Let’s consider a rectangle with a width of 4 units and a length of 2 units.
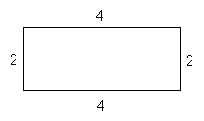
Let’s divide each side into segments with a length of 1, as below.
Now, using these divisions, we’ll draw a grid that divides up the rectangle.
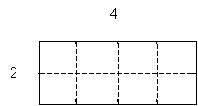
Note that the grid is divided into smaller regions whose each side has a length of 1 unit.
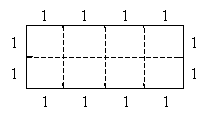
Each of these smaller regions is a square (a rectangle whose length and width are equal) with sides of length 1. We define one of these regions as 1 square unit-a square whose dimensions (length and width) are both 1 unit. Now, notice that the rectangle has a total of 8 square units, which are divided into two rows of four or four rows of two (depending on how you view the diagram). But calculating the number of objects (square units, in this case) in rows and columns can be done by multiplication: notice that the number of square units in the rectangle is simply the product of the length and the width. Thus, the area A of a rectangle with length l and width w is the product of l and w:
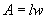
This formula applies to any rectangle, regardless of the lengths of its sides. (That is, the lengths can be positive integers, fractions, decimals, rational numbers, or irrational numbers.)
For instance, let’s say we had a rectangle with a length of 5 inches and a width of 3 inches, as shown below.
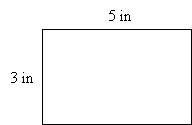
Our goal is to calculate how many squares having sides of length 1 inch can fit into this rectangle–the result is the total area of the rectangle. Placing the squares edge to edge, we can fit five of them across the rectangle, and we can fit three down the rectangle.
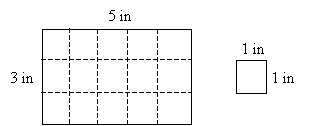
We can see from the diagram that we can fit 15 one-square-inch squares into the rectangle–thus, the rectangle has an area of 15 square inches. Of course, this is what the formula indicates as well:

Practice Problem: Calculate the area of a rectangle with width 32 inches and length ![]() inch.
inch.
Solution: The area formula for a rectangle applies regardless of the numbers used (as long as they are positive, of course). Thus, let’s simply use the formula for the area A:
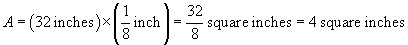
Triangles
We can also consider some characteristics of another common geometric figure: the triangle. A triangle is a closed geometric figure with three sides; examples of triangles are shown below.
The perimeter of a triangle is calculated in much the same way as the perimeter of a rectangle: simply add the lengths of the sides of the triangle (in this case, the figure has only three sides, and these sides can all be different lengths). Calculating the area, however, is somewhat more difficult. For rectangles, we were able to see the area as simply rows and columns of squares. Because of the shape of a triangle, we cannot neatly fit the squares into it.
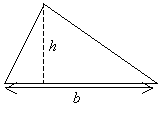
We must take a slightly different approach to finding the area of a triangle. Let’s consider a generic triangle shown below; this triangle has no particularly special properties.

Now, let’s identify two characteristic dimensions of this (or any) triangle: the length of the base (which we’ll call b) and the height (which we’ll call h). The base is simply the length of the side “on the ground,” or at the bottom of the figure. The height is then the maximum distance that the triangle reaches “above the ground.”
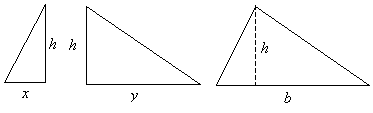
The area of the triangle is A. If we had two such triangles of exactly the same shape, the total area of the two triangles would then be 2A. Let’s use this fact to try to construct a more familiar figure.
First, we’ll cut one of the triangles along its height.
Notice that the divided triangles both have heights h (just as we defined for the original triangle) and that their bases are x and y, where x + y is equal to b. We do not know what x and y are, but because we cut the triangle, we know that these two bases must sum to the base of the original triangle. Now, let’s try rearranging the pieces to make a rectangle!
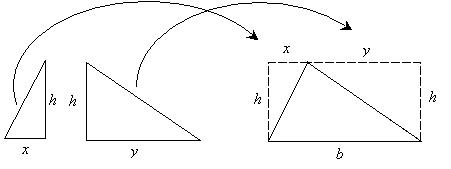
Let’s now consider the characteristics of this new figure (remember, it has an area 2A, where A is the area of the original triangle).
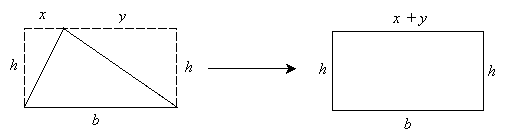
The figure is a rectangle-note that opposite sides are equal in length (remember that x + y = b). But we know how to calculate the area of a rectangle: it is simply the product of the length and width (b and h in this case). This total area, however, is twice the area of the original triangle. Thus, the product of b and h is equal to 2A.
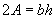
From our study of linear equations, we learned how to solve for a particular variable. In this case, we can isolate A by multiplying both sides of the expression by ![]() .
.
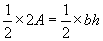
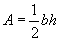
Thus, we have derived a formula for the area of a triangle. This derivation, although not shown in its full mathematical rigor, produces the correct area formula for all triangles, not just the one shown above. The process of calculating the height h of a triangle can be somewhat complicated, but if you know the base and height, you are now able to calculate the area of the triangle.
Practice Problem: Calculate the area of the triangle below.
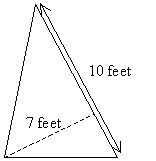
Solution: If we rotate the triangle so that the 10-foot side is on the bottom, we see that the dashed line segment represents the height of the triangle.
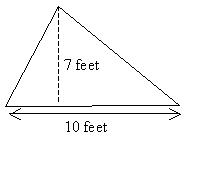
We can then calculate the area of the triangle using the formula we derived in the lesson.