But first, I would like to thank you for stopping by! You might have come to this article because you are interested in learning more about How To Convert Hexadecimal To Binary. Or perhaps you want to learn how to convert hexadecimal to binary calculator? If you are, good job!
Table of Contents
Hexadecimal System (Hex System)
The hexadecimal system (shortly hex), uses the number 16 as its base (radix). As a base-16 numeral system, it uses 16 symbols. These are the 10 decimal digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) and the first six letters of the English alphabet (A, B, C, D, E, F). The letters are used because of the need to represent the values 10, 11, 12, 13, 14 and 15 each in one single symbol.
Hex is used in mathematics and information technologies as a more friendly way to represent binary numbers. Each hex digit represents four binary digits; therefore, hex is a language to write binary in an abbreviated form.
Four binary digits (also called nibbles) make up half a byte. This means one byte can carry binary values from 0000 0000 to 1111 1111. In hex, these can be represented in a friendlier fashion, ranging from 00 to FF.
In html programming, colors can be represented by a 6-digit hexadecimal number: FFFFFF represents white whereas 000000 represents black. https://43b42244a5ce62cd50b6105f0f90636f.safeframe.googlesyndication.com/safeframe/1-0-38/html/container.html
Binary System
The binary numeral system uses the number 2 as its base (radix). As a base-2 numeral system, it consists of only two numbers: 0 and 1.
While it has been applied in ancient Egypt, China and India for different purposes, the binary system has become the language of electronics and computers in the modern world. This is the most efficient system to detect an electric signal’s off (0) and on (1) state. It is also the basis for binary code that is used to compose data in computer-based machines. Even the digital text that you are reading right now consists of binary numbers.
Reading a binary number is easier than it looks: This is a positional system; therefore, every digit in a binary number is raised to the powers of 2, starting from the rightmost with 20. In the binary system, each binary digit refers to 1 bit.
How do you change those funny numbers and letters to something you or your computer can understand? Converting hexadecimal to binary is very easy, which is why hexadecimal has been adopted in some programming languages. Converting to decimal is a little more involved, but once you’ve got it it’s easy to repeat for any number.
Part 1 Converting Hexadecimal to Binary
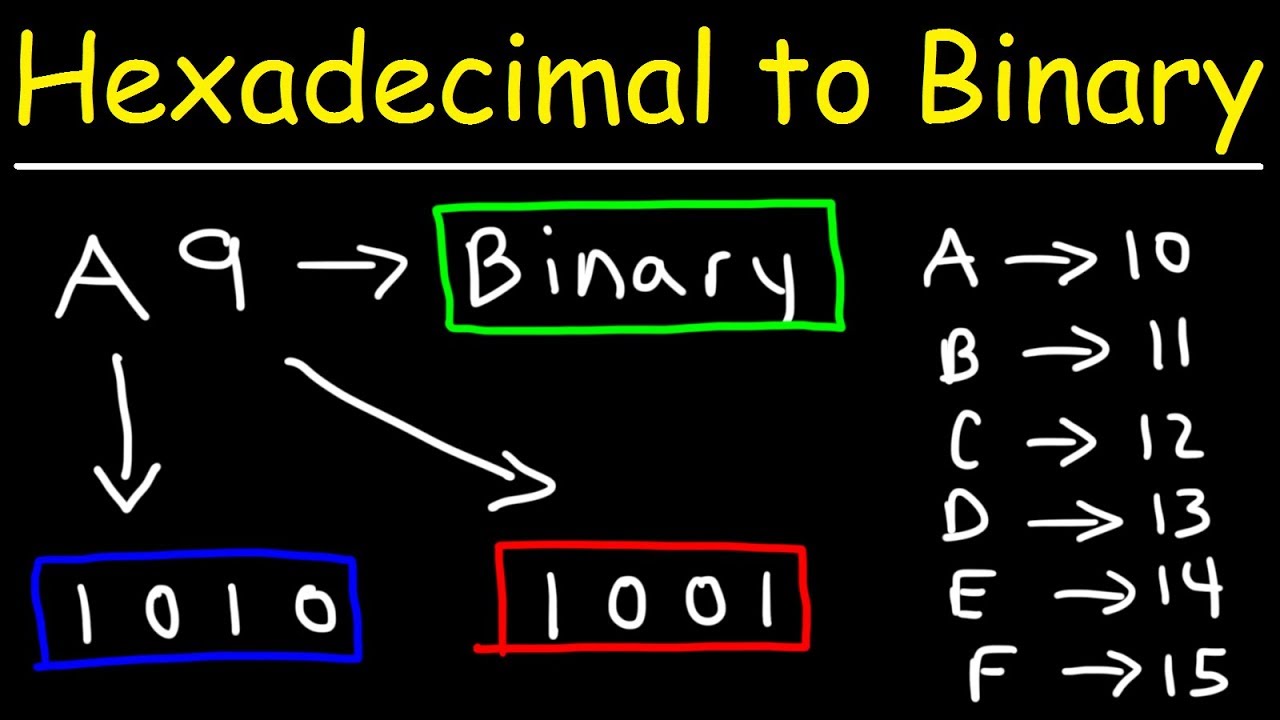
- 1 Convert each hexadecimal digit to four binary digits. Hexadecimal was adopted in the first place because it’s so easy to convert between the two. Essentially, hexadecimal is used as a way to display binary information in a shorter string. This chart is all you need to convert from one to the other:
| Hexadecimal | Binary |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
- 2 Try it yourself. It really is as simple as changing the digit into the four equivalent binary digits. Here are a few hex numbers for you to convert. Highlight the invisible text to the right of the equal sign to check your work:
- A23 = 1010 0010 0011
- BEE = 1011 1110 1110
- 70C558 = 0111 0000 1100 0101 0101 1000
- 3 Understand why this works. In the “base two” binary system, n binary digits can be used to represent 2n different numbers. For example, with four binary digits, you can represent 24 = 16 different numbers. Since hexadecimal is a base sixteen system, a one digit number can be used to represent 161 = 16 different numbers. This makes conversion between the two systems extremely easy.[2]
- You can also think of this as the counting systems “flipping over” to another digit at the same time. Hexadecimal counts “…D, E, F, 10” at the same time binary counts “1101, 1110, 1111, 10000“.
Part 2 Converting Hexadecimal to Decimal
- 1 Review how base ten works. You use decimal notation every day without having to stop and think about the meaning, but when you first learned it, your parent or teacher might have explained it to you in more detail. A quick review of how ordinary numbers are written will help you convert the number:[3]
- Each digit in a decimal number is in a certain “place.” Moving from right to left, there’s the “ones place,” “tens place,” “hundreds place,” and so on. The digit 3 just means 3 if it’s in the ones place, but it represents 30 when located in the tens place, and 300 in the hundreds place.
- To put it mathematically, the “places” represent 100, 101, 102, and so on. This is why this system is called “base ten,” or “decimal” after the Latin word for “tenth.”
- 2 Write a decimal number as an addition problem. This will probably seem obvious, but it’s the same process we’ll use to convert a hexadecimal number, so it’s a good starting point. Let’s rewrite the number 480,13710. (Remember, the subscript 10 tells us the number is written in base ten.):
- Starting with the rightmost digit, 7 = 7 x 100, or 7 x 1
- Moving left, 3 = 3 x 101, or 3 x 10
- Repeating for all digits, we get 480,137 = 4×100,000 + 8×10,000 + 0x1,000 + 1×100 + 3×10 + 7×1.
- 3 Write the place values next to a hexadecimal number. Since hexadecimal is base sixteen, the “place values” correspond to the powers of sixteen. To convert to decimal, multiply each place value by the corresponding power of sixteen. Start this process by writing the powers of sixteen next to the digits of a hexadecimal number. We’ll do this for the hexadecimal number C92116. Start on the right with 160, and increase the exponent each time you move left to the next digit:[4]
- 116 = 1 x 160 = 1 x 1 (All numbers are in decimal except where noted.)
- 216 = 2 x 161 = 2 x 16
- 916 = 9 x 162 = 9 x 256
- C = C x 163 = C x 4096
- 4 Convert alphabetic characters to decimal. Numerical digits are the same in decimal or hexadecimal, so you don’t need to change them (for instance, 716 = 710). For alphabetic characters, refer to this list to change them to the decimal equivalent:
- A = 10
- B = 11
- C = 12 (We’ll use this on our example from above.)
- D = 13
- E = 14
- F = 15
- 5 Perform the calculation. Now that everything is written in decimal, perform each multiplication problem and add the results together. A calculator will be handy for most hexadecimal numbers. Continuing our example from earlier, here’s C921 rewritten as a decimal formula and solved:[5]
- C92116 = (in decimal) (1 x 1) + (2 x 16) + (9 x 256) + (12 x 4096)
- = 1 + 32 + 2,304 + 49,152.
- = 51,48910. The decimal version will usually have more digits than the hexadecimal version, since hexadecimal can store more information per digit.
- 6 Practice the conversion. Here are a few numbers to convert from hexadecimal into decimal. Once you’ve worked out the answer, highlight the invisible text to the right of the equal sign to check your work:
- 3AB16 = 93910
- A1A116 = 4137710
- 500016 = 2048010
- 500D16 = 2049310
- 18A2F16 = 10091110
Part 3 Understanding Hexadecimal Basics
- 1 Know how to use hexadecimal. Our ordinary decimal counting system is base ten, using ten different symbols to display numbers. Hexadecimal is a base sixteen number system, meaning it uses sixteen characters to display numbers.You can check hexadecimal to decimal conversion for big numbers on online tools.[6]
- Counting from zero upward:
| Hexadecimal | Decimal | Hexadecimal | Decimal |
|---|---|---|---|
| 0 | 0 | 10 | 16 |
| 1 | 1 | 11 | 17 |
| 2 | 2 | 12 | 18 |
| 3 | 3 | 13 | 19 |
| 4 | 4 | 14 | 20 |
| 5 | 5 | 15 | 21 |
| 6 | 6 | 16 | 22 |
| 7 | 7 | 17 | 23 |
| 8 | 8 | 18 | 24 |
| 9 | 9 | 19 | 25 |
| A | 10 | 1A | 26 |
| B | 11 | 1B | 27 |
| C | 12 | 1C | 28 |
| D | 13 | 1D | 29 |
| E | 14 | 1E | 30 |
| F | 15 | 1F | 31 |
- 2 Use subscript to show which system you’re using. Whenever it might be unclear which system you’re using, use a decimal subscript number to denote the base. For example, 1710 means “17 in base ten” (an ordinary decimal number). 1710 = 1116, or “11 in base sixteen” (hexadecimal). You can skip this if your number has an alphabetic character in it, such as B or E. No one will mistake that for a decimal number.
Conclusion
Hexadecimal to binary converter is a software that converts the hexadecimal values to binary values. It convert 16 bit data per time. Hexadecimal number consists of four characters, i.e 0-9 and A-F. The numbers are also represented with two numbers per character. So, they are known as base 16 numbers.