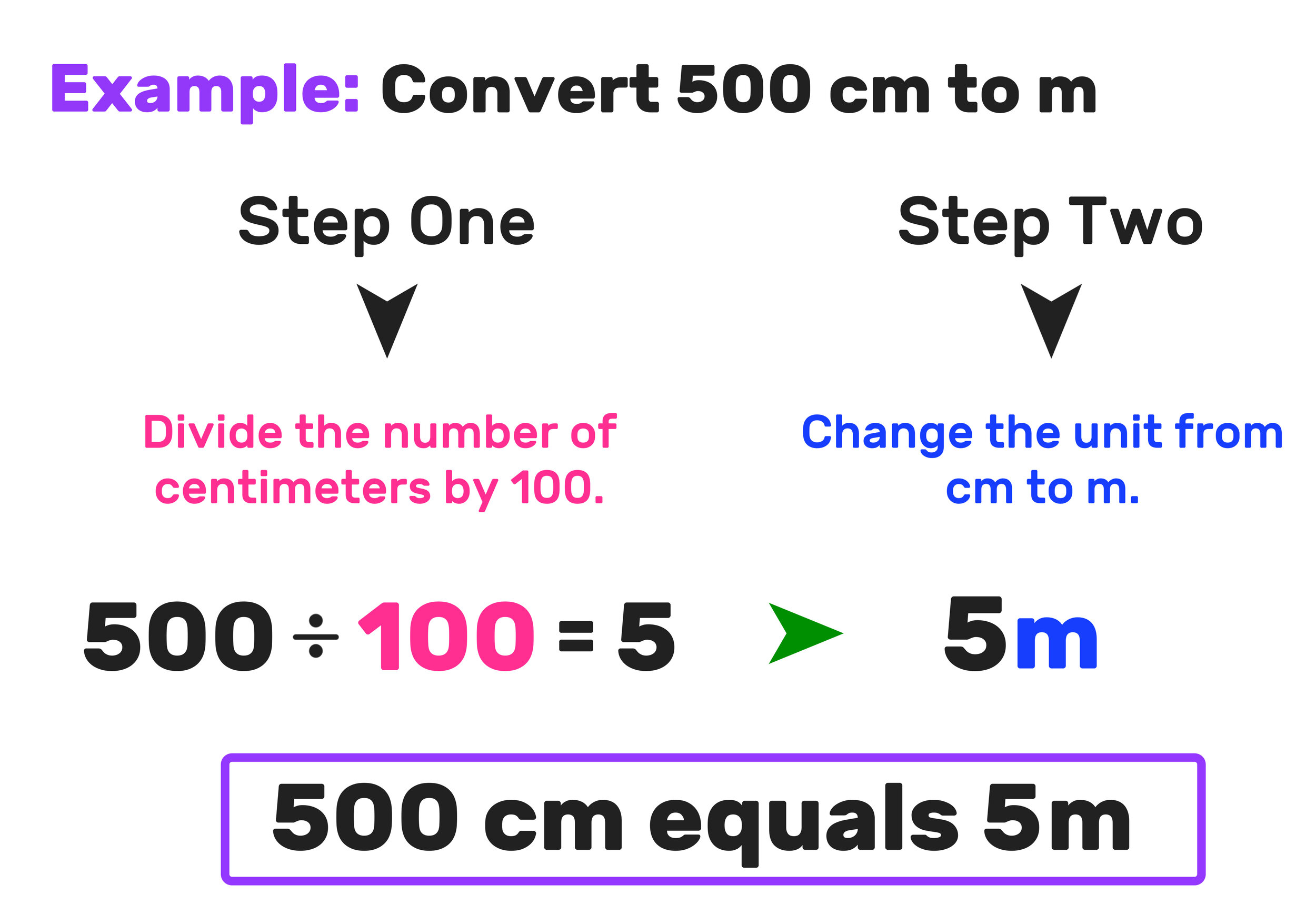
There is a straight-forward way to convert cm to m for any units you choose. The formula is a simple one and it will be helpful for converting distances of many units while doing physics problems or homework. Welcome to this article, here you will learn How To Convert Cm To M.
Centimeters (cm) and meters (m) are both measurements of distance in the metric system. There are 100 centimeters in every meter, which means that dividing your measurement in centimeters by 100 will convert it to meters. You can make this conversion quick and easy by simply moving the decimal point in your measurement 2 spaces (or “place values”) to the left. Likewise, if you need to convert from meters to centimeters instead, simply move the decimal point 2 spaces to the right!
Table of Contents
Method 1 Converting from Centimeters to Meters Download Article
- Interpret “centimeter” as “1/100 meters” when you see it. The prefix “centi-” means “one-hundredth,” so a centimeter equates to 1/100 of a meter. This means that converting from centimeters to meters always involves dividing by 100. Similarly, converting from meters to centimeters always involves multiplying by 100.[1]
- Likewise, a millimeter is 1/1000 meters (since “milli-” means “one-thousandth”) and a kilometer is 1000 meters (since “kilo-” means “one thousand”).
- Locate the decimal point or inferred decimal point in your starting number. For instance, if your starting measurement is 872.5 centimeters (cm), then the decimal point is clearly located between the 2 and the 5. However, if your starting measurement is 63 cm, then the decimal point is inferred—to make it visible, rewrite the number as 63.0 cm.[2]
- The decimal point always appears between the “ones” (to its left) and “tenths” (to its right) place values in a number. In 82.5, for example, 2 is in the ones place and 5 is in the tenths place.
- If your starting measurement is written as a fraction, such as 872 ½ cm, rewrite it in decimal form as 872.5 cm. Similarly, 4 ¼ cm equals 4.25 cm, and 4 ⅓ cm is approximately 4.33 cm.
- Slide the decimal point 2 spaces to the left. In the case of 872.5, moving the decimal point 2 spaces to the left results in 8.725. This is the measurement in meters, so your answer is 872.5 cm = 8.725 m.[3]
- If your starting measurement is 63 cm (that is, 63.0 cm), sliding the decimal 2 spaces to the left results in 0.63. Therefore, 63 cm = 0.63 m.
- Add zeros to the left as needed when sliding the decimal point. For example, if your starting number is 4.25 cm, there’s only one digit to the left of the decimal point. In this case, add a zero to the left as you slide the decimal point over. Therefore, 4.25 cm = 0.0425 m.[4]
- Similarly, 0.3 cm = 0.003 m.
- Divide the number of centimeters by 100 for a quick solution. If you don’t want to mess around with place value, simply divide the number of centimeters by 100 to figure out how many meters it equals.[5]
- For instance, converting from 82.5 to 0.825 involves shifting the decimal point 2 place values to the left, which is the same as dividing by 100.
- Practice doing word problems to build your skills. For example: “Joe measures several short lengths of rope and finds that he has 7890 cm of rope in total. How many meters of rope does Joe have?”[6]
- There’s no obvious decimal point here, but remember that 7890 is the same as 7890.0.
- Move the decimal point 2 spaces to the left to get your answer: 7890 cm = 78.90 m.
- Completing a long division calculation for 7890 / 100 confirms this result.
Method 2 Converting from Meters to Centimeters Download Article
- Locate the decimal point or inferred decimal point in the starting number. For example, if your starting measurement is 2.3 m, the decimal point is located between the 2 and the 3.[7]
- However, if your starting measurement is 23 m, the decimal point is inferred to be after the 23. If you wish, you can rewrite 23 m as 23.0 m.
- Slide the decimal point 2 places to the right. To convert from meters to centimeters, simply slide the decimal point 2 spaces in the opposite direction. For example:[8]
- 2.3 m = 230 cm (add zeros to the right as needed)
- 0.45 m = 45 cm
- 12.2 m = 1220 cm
- 0.01 m = 1 cm
- Multiply the number of meters by 100 for an alternative option. If you need to convert from meters to centimeters instead of the other way around, you must multiply by 100 instead of dividing by 100. As when dividing by factors of 10, the number of spaces (or “place values”) you slide the decimal point equals the number of zeros in the factor of 10 (the divisor). This time, though, you slide the decimal right instead of left.[9]
- So, 82.5 x 100 = 8250, with the decimal point shifted 2 places to the right (which is equal to the number of zeros in 100).
- Similarly, 82.5 x 10 = 825 and 82.5 x 1000 = 82500.
- Practice doing word problems so you don’t get tripped up. Make sure you don’t move the decimal points the wrong direction when you’re converting from meters to centimeters (or vice versa)! Doing practice word problems is the best way to avoid this mistake. For example: “Henry’s old garden fence is 16 meters long, but the new fencing he wants to buy is sold by the centimeter. How many centimeters of fencing does Henry need?”[10]
- Rewrite 16 as 16.0 so you can visualize the decimal point.
- Add another zero to the end (16.0 → 16.00) so you can slide the decimal point 2 places to the right.
- Therefore, 16 m = 1600 cm. Henry needs 1600 cm of fencing.
- Multiplying 16 x 100 confirms this result.
Centimeter
Definition: A centimeter (symbol: cm) is a unit of length in the International System of Units (SI), the current form of the metric system. It is defined as 1/100 meters.
History/origin: A centimeter is based on the SI unit meter, and as the prefix “centi” indicates, is equal to one hundredth of a meter. Metric prefixes range from factors of 10-18 to 1018 based on a decimal system, with the base (in this case the meter) having no prefix and having a factor of 1. Learning some of the more commonly used metric prefixes, such as kilo-, mega-, giga-, tera-, centi-, milli-, micro-, and nano-, can be helpful for quickly navigating metric units.
Current use: The centimeter, like the meter, is used in all sorts of applications worldwide (in countries that have undergone metrication) in instances where a smaller denomination of the meter is required. Height is commonly measured in centimeters outside of countries like the United States.
Meter
Definition: A meter, or metre (symbol: m), is the base unit of length and distance in the International System of Units (SI). The meter is defined as the distance traveled by light in 1/299 792 458 of a second. This definition was slightly modified in 2019 to reflect changes in the definition of the second.
History/origin: Originally, in 1793, the meter was defined as one ten-millionth of the distance from the equator to the North Pole. This changed in 1889, when the International prototype metre was established as the length of a prototype meter bar (made of an alloy of 90% platinum and 10% iridium) measured at the melting point of ice. In 1960, the meter was again redefined, this time in terms of a certain number of wavelengths of a certain emission line of krypton-86. The current definition of the meter is effectively the same as the definition that was adopted in 1983, with slight modifications due to the change in definition of the second.
Current use: Being the SI unit of length, the meter is used worldwide in many applications such as measuring distance, height, length, width, etc. The United States is one notable exception in that it largely uses US customary units such as yards, inches, feet, and miles instead of meters in everyday use.
Centimeter to Meter Conversion Table
| Centimeter [cm] | Meter [m] |
|---|---|
| 0.01 cm | 0.0001 m |
| 0.1 cm | 0.001 m |
| 1 cm | 0.01 m |
| 2 cm | 0.02 m |
| 3 cm | 0.03 m |
| 5 cm | 0.05 m |
| 10 cm | 0.1 m |
| 20 cm | 0.2 m |
| 50 cm | 0.5 m |
| 100 cm | 1 m |
| 1000 cm | 10 m |
Conclusion
The international system of units bases its measures of length on a single prototype: the meter. No other unit is based on a single physical prototype. The International Bureau of Weights and Measures has acknowledged this variation by allowing any number of authoritative conversions of the meter into a definitive list of finished units.