Have you ever wondered how two numbers in binary form – 01011110 and 1100110 converted to the world’s most famous number system, the decimal? Or How To Convert Binary To Hexadecimal? Is it the same calculation method when converting binary to hexadecimal? How do you convert 2-digit binary to hex? All of these questions are important when implementing your app. Our goal is to provide answers about convert binary to hexadecimal with an example of using the conversion formula with the programmatic conversion.
This article will explain how to convert binary (base 2) to hexadecimal (base 16). Whether it is for coding, for math class, or for The Martian, hexadecimal is a useful and powerful shortcut when writing long binary strings. Since both bases are powers of 2, this procedure is much simpler than general conversions such as converting decimal to binary. All you need are basic adding and counting skills to make turn a binary number into hexadecimal.
Binary is the simplest kind of number system that uses only two digits of 0 and 1 (i.e. value of base 2). Since digital electronics have only these two states (either 0 or 1), so binary number is most preferred in modern computer engineer, networking and communication specialists, and other professionals.
Whereas Hexadecimal number is one of the number systems which has value is 16 and it has only 16 symbols − 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and A, B, C, D, E, F. Where A, B, C, D, E and F are single bit representations of decimal value 10, 11, 12, 13, 14 and 15 respectively.
Table of Contents
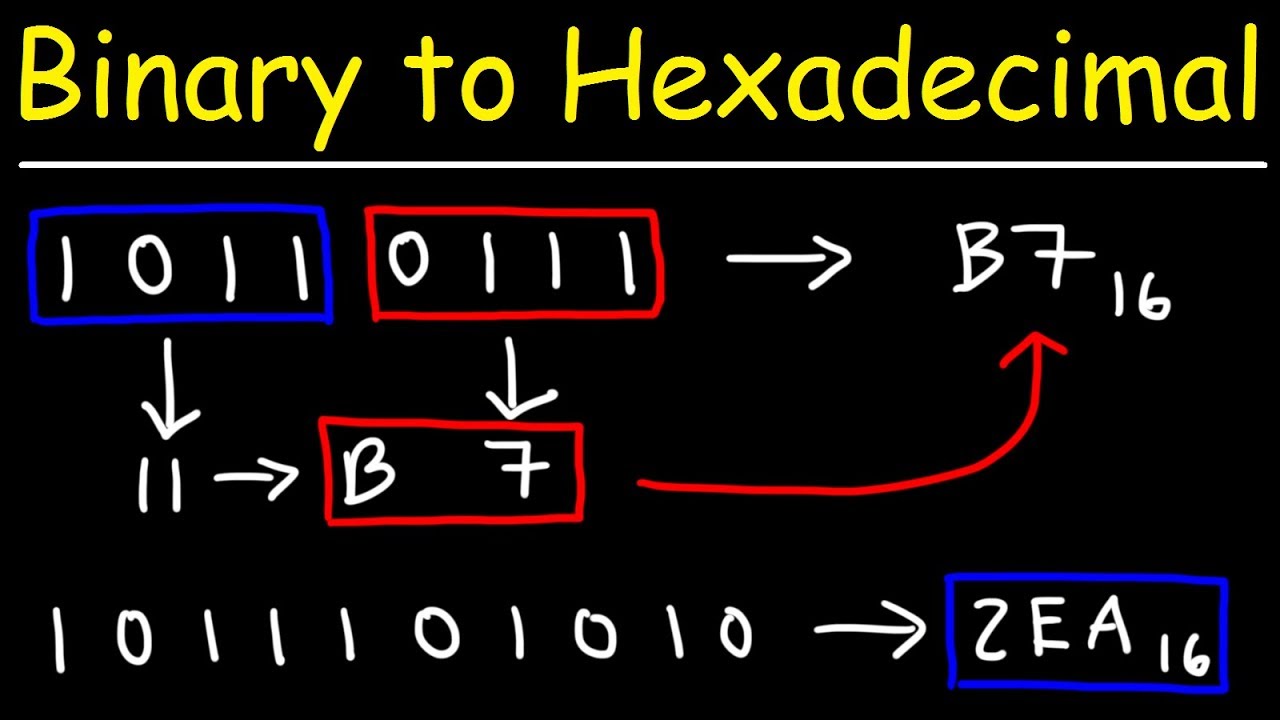
Conversion from Binary to Hexadecimal number system
Hexadecimal number system provides convenient way of converting large binary numbers into more compact and smaller groups. There are various ways to convert a binary number into hexadecimal number. You can convert using direct methods or indirect methods. First, you need to convert a binary into other base system (e.g., into decimal, or into octal). Then you need to convert it hexadecimal number.
| Most Significant Bit (MSB) | Hexa Point | Least Significant Bit (LSB) | |||
|---|---|---|---|---|---|
| 162 | 161 | 160 | 16-1 | 16-2 | 16-3 |
| 256 | 16 | 1 | 1/16 | 1/256 | 1/4096 |
Since number numbers are type of positional number system. That means weight of the positions from right to left are as 160, 161, 162, 163and so on. for the integer part and weight of the positions from left to right are as 16-1, 16-2, 16-3and so on. for the fractional part.
Method 1Method 1 of 2:Making Basic Conversions
- Find a line of up to four binary numbers to convert. Binary numbers can only be 1 and 0. Hexadecimal numbers can be 0-9, or A-F, since hexadecimal is base-16. You can convert any binary string to hexadecimal (1, 01, 101101, etc.), but you need four numbers to make the conversion (0101→5; 1100→C, etc.). For this lesson, start with the example 1010.
- 1010
- If you don’t have 4 digits, add zeros to the front to make it four digits. So, 01 would become 0001.[1]
- Write a small “1” above the last digit. Each of the four numbers signifies a type of number decimal system number. The last digit is the one’s place. You will make sense of the rest of the digits in the next step. For now, write a small one above the last digit.[2]
- 1010
- {\displaystyle 1010^{1}}
- Note that you are not raising anything to any power — this is just a way to see what digit means what.
- Write a small “2” above the third digit, a “4” above the second, and an “8” above the first. These are the rest of your place holders. If you’re curious, this is because each digit represents a different power of 2. The first is {\displaystyle 2^{3}}
, the second {\displaystyle 2^{2}}
, etc.
- 1010
- {\displaystyle 1^{8}0^{4}1^{2}0^{1}}. If the length is less than 4, then you need to add zeros on the left and make a number four digits long.[3]
- Count out how many of each “place” you have. Luckily, this conversion is easy once you have four numbers and know what they all mean. If you have a one in the first number, you have one eight. If you have a zero in the second column, you have no fours. The third column tells you how many twos, and the second how many ones. So, for our example:[4]
- 1010
- {\displaystyle 1^{8}0^{4}1^{2}0^{1}}
- 8 0 2 0
- Add your four numbers together. Once you have your new hexadecimal numbers, simply add them up.
- 1010
- {\displaystyle 1^{8}0^{4}1^{2}0^{1}}
- 8 0 2 0
- {\displaystyle 8+0+2+0=10}
- Final answer: The binary number 1010 converts to A in the hexadecimal system.
- Change any number above “9” into a letter. This is so you don’t get confused when reading hexadecimal (“is that a 1 and a 5, or a 15?”). Luckily, the system is super easy, since you can’t have a hexadecimal number bigger than 15. Simply start the alphabet with 10, so that:
- {\displaystyle 10=A}
- {\displaystyle 11=B}
- {\displaystyle 12=C}
- {\displaystyle 13=D}
- {\displaystyle 14=E}
- {\displaystyle 15=F}
- {\displaystyle 10=A}
- Try a few examples to get better at converting. The following examples have answers in white beneath them. To see the work and the answers, highlight the area under the question by clicking and dragging your mouse over it.
- Convert 1 to hexadecimal.
- Add zeros to get four digits: 0001
- Find your place holders: {\displaystyle 0^{8}0^{4}0^{2}1^{1}}
- Add up the digits: {\displaystyle 0+0+0+1=1}
- Final answer: 1
- Convert 0101 to hexadecimal.
- Add zeros to get four digits: 0101
- Find your place holders: {\displaystyle 0^{8}1^{4}0^{2}1^{1}}
- Add up the digits: {\displaystyle 0+4+0+1=5}
- Final answer: 5
- Convert 1110 to hexadecimal.
- Add zeros to get four digits: 1110
- Find your place holders: {\displaystyle 1^{8}1^{4}1^{2}0^{1}}
- Add up the digits: {\displaystyle 8+4+2+0=14}
- Final answer: E
- Convert 1011 to hexadecimal.
- Add zeros to get four digits: 1011
- Find your place holders: {\displaystyle 1^{8}0^{4}1^{2}1^{1}}
- Add up the digits: {\displaystyle 8+0+2+1=11}
- Final Answer: BAdvertisement
- Convert 1 to hexadecimal.
Method 2Method 2 of 2:Converting Long Binary Strings
- Cut your string of binary numbers into groups of four, starting from the right. Hexadecimal converts 4 binary digits into one hexadecimal unit. So, in order to convert the number, you first need to break it up into groups of four, starting on the right. For example:
- Convert {\displaystyle 11101100101001}
into a hexadecimal number.
- {\displaystyle 11101100101001=(11)(1011)(0010)(1001)}
- Convert {\displaystyle 11101100101001}
- Add extra zeros to the front of the first number if it is not four digits. The zeros will not affect the conversion, but they will make it easier to visualize. Remember, you want all groups of 4-digit binary numbers.
- Convert {\displaystyle 11101100101001}
into a hexadecimal number.
- {\displaystyle 11101100101001=(11)(1011)(0010)(1001)}
- {\displaystyle (11)(1011)(0010)(1001)=}
{\displaystyle (0011)(1011)(0010)(1001)}
- Convert {\displaystyle 11101100101001}
- Convert one 4-digit group at a time. You’ll need to convert each binary set by itself, so separate them on your paper to make them easier to work with. Work on converting each individual string of four into its hexadecimal counterpart. For our example:[5]
- {\displaystyle 0011=0+0+2+1=3}
- {\displaystyle 1011=8+0+2+1=11=B}
- {\displaystyle 0010=0+0+2+0=2}
- {\displaystyle 1001=8+0+0+1=9}
- {\displaystyle 0011=0+0+2+1=3}
- Remove the spaces to create your hexadecimal number. Once you’ve converted all the 4-digit parts, simply ram them together to get your final answer. So, for the example above:
- {\displaystyle (0011)(1011)(0010)(1001)}
- 3 B 2 9
- {\displaystyle 11101100101001=3B29}
- {\displaystyle (0011)(1011)(0010)(1001)}
- Memorize or check a conversion table to see if you got each part right. There are only 16 possible 4-digit combinations of binary numbers. So, if you don’t want to figure out each string individually, you can use this conversion table [6] .https://5e4ca2894c757dd6202f025e6bb88977.safeframe.googlesyndication.com/safeframe/1-0-38/html/container.htmlAdvertisement
| Binary | Hexadecimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Conclusion
A binary number is just a number represented as 0s and 1s. For example, the decimal number 359 can be represented as 3 1001 in binary form. You might wonder where this article is heading; it is surprising how many different applications lurk behind this seemingly basic concept of binary numbers.