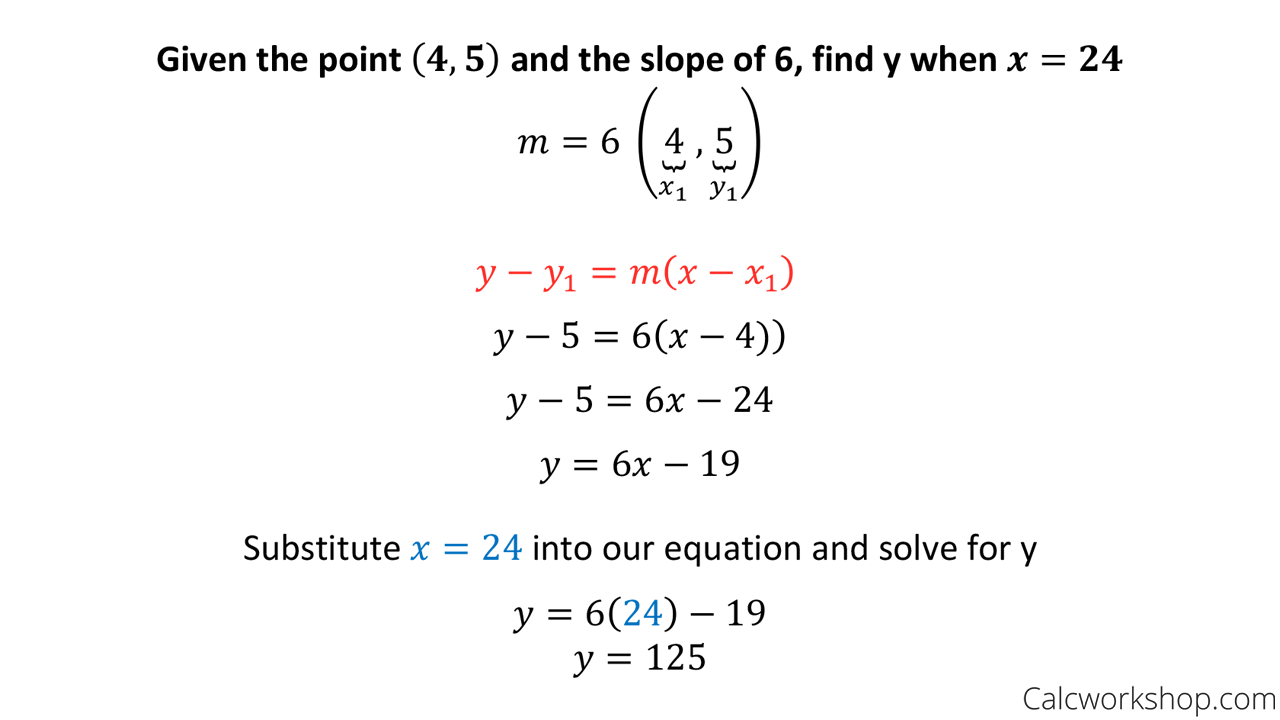How to Write Point-Slope Form – Algebra is a wonderful subject and curve fitting is a recurring problem when working with this subject. So, this post is going to show you How to Write Point-Slope Form in a very easy way.
We can also find the equation of a line when given the slope and any point (not the y-intercept), and there are two methods to do so. The following video will use a single example to show how to use both methods to find the equation of a line with a given slope and single point.
These are the two methods to finding the equation of a line when given a point and the slope:
- Substitution method = plug in the slope and the (x, y) point values into y = mx + b, then solve for b. Use the m given in the problem, and the b that was just solved for, to create the equation y = mx + b.
- Point-slope form = y−y1=m(x−x1), where (x1,y1) is the point given and m is the slope given. The ‘x’ and the ‘y’ stay as variables.
The point slope form is used to find the equation of the straight line which is inclined at a given angle to the x-axis and passes through a given point. The equation of a line is an equation that is satisfied by each and every point on the line. This means that a linear equation in two variables represents a line. The equation of a line can be found through various methods depending on the available information. Some of the methods are:
- Point slope form
- Slope-intercept form
- Intercept form
- Two-point form
Point slope formula is used only when we know the slope of the line and a point on the line. Let us learn about the point slope form and how to derive the formula to represent point slope form in detail in the following section.
Table of Contents
What is Point Slope Form?
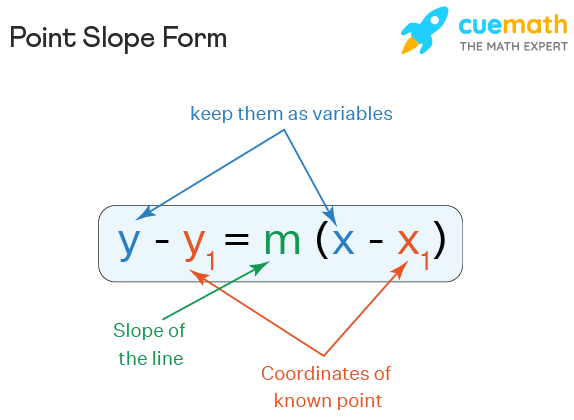
Point slope form is used to represent a straight line using its slope and a point on the line. That means, the equation of a line whose slope is ‘m’ and which passes through a point (x11, y11) is found using the point slope form. Different forms can be used to express the equation of a straight line. One of them is point slope form. The equation of the point slope form is:
y – y11 = m(x – x11)
where, (x, y) is a random point on the line and m is the slope of the line.
Point Slope Formula
The point slope form formula is used to find the equation of a line. The equation of a line with a given slope and with a given point is found using the point slope form. This formula is used only when we know the slope of the line and a point on the line. We have some other formulas as well to find the equation of a line such as slope-intercept form, intercept form, etc. Here is the point slope formula,
Point Slope Formula in Math:
y − y11 = m (x − x11)
where,
- (x, y) is a random point on the line(which should be kept as variables while applying the formula).
- (x11, y11) is a fixed point on the line.
- m is the slope of the line.
Derivation of Point Slope Formula
Let us see how to find the point slope form (i.e. the proof of the formula of the point slope form). We will derive this formula using the equation for the slope of a line. Let us consider a line whose slope is ‘m’. Let us assume that (x11, y11) is a known point on the line. Let (x, y) be any other random point on the line whose coordinates are not known.
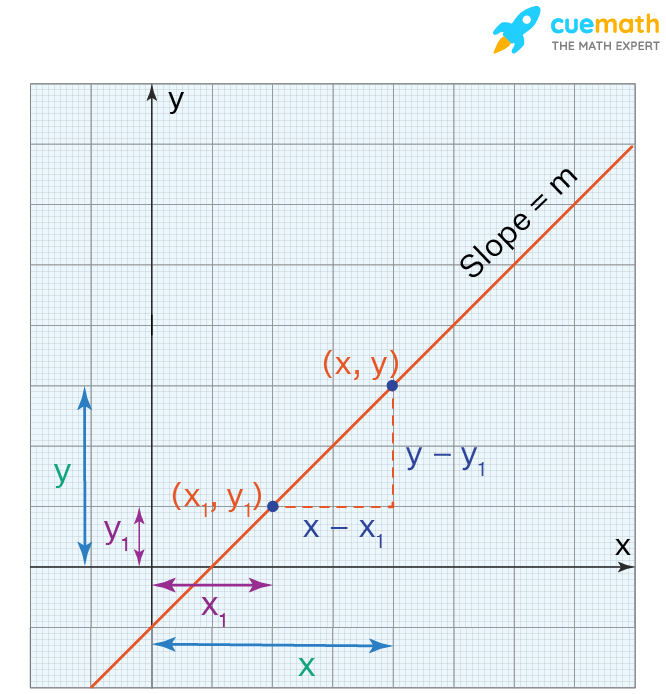
We know that the equation for the slope of a line is:
Slope = (Difference in y-coordinates)/(Difference in x-coordinates)
m = (y – y11)/(x – x11)
Multiplying both sides by (x – x11),
m(x – x11) = y – y11
This can be written as,
y – y11 = m(x – x11)
Hence the point slope formula is proved.
Point Slope Formula Examples
Some examples of the point slope form formula are shown here.
- The equation of a line with slope (-1) and a point (1, 2) is found using: y – 2 = (-1)(x – 1).
- The equation of a line with slope (3/2) and a point (-1/2, 2/3) is found using: y – (2/3) = (3/2) (x – (-1/2)).
- The equation of a line with slope (0) and a point (3, -2) is found using: y – (-2) = 0(x – 3).
In each of these cases, we can simplify the equation further and get it to the form: y = mx + b.
Important notes on Point Slope Form:
- The equation of the point slope form of a line whose slope is ‘m’ and that passes through a point (x11, y11) is y – y11 = m(x – x11).
- The equation of a horizontal line passing through (a, b) is of the form y = b.
- The equation of a vertical line passing through (a, b) is of the form x = a.
This is an exceptional case where the point slope form cannot be used.
How to Solve Point Slope Form?
To solve point slope form for a given straight line for finding the equation of the given line, we can follow the steps given below,
- Step 1: Note down the slope, ‘m’ of the straight line, and the coordinates(x11, y11) of the given point that lies on the line.
- Step 2: Substitute the given values in the point slope formula: y – y11 = m(x – x11).
- Step 3: Simplify to obtain the equation of the line in standard form.
☛ Also Check: You can try this point slope form calculator to verify the result obtained for the equation of a line segment- Point-Slope Form Calculator
Let us see an example to understand the application of above steps on point slope form.
Example: Find the equation of a line that passes through a point (2, -3) and whose slope is (-1/2).
Solution:
The point on the given line is: (x11, y11) = (2, -3)
The slope of the line is: m = (-1/2)
The equation of the line is found using the point slope form:
y − y11 = m(x − x11)
y − (−3) = (−1/2)(x − 2)
y + 3 = (−1/2)x + 1
Subtracting 3 from both sides,
y = (−1/2)x − 2
Thus, the equation of the required line is, y = (−1/2)x − 2
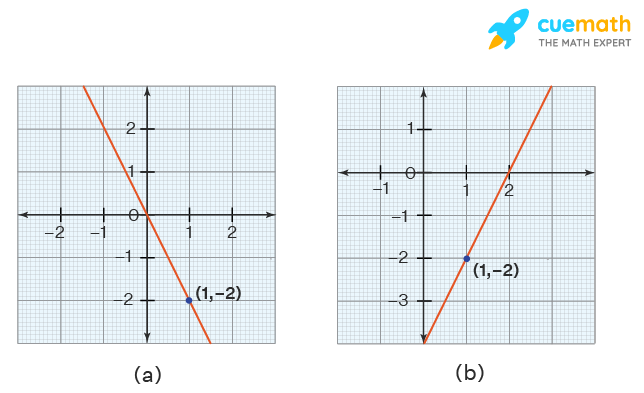
Thinking out of the box:
Which of the following graphs may represent the equation y + 2 = −2(x − 1)?
What About y = mx + b ?
You may already be familiar with the “y=mx+b” form (called the slope-intercept form of the equation of a line).
It is the same equation, in a different form!
The “b” value (called the y-intercept) is where the line crosses the y-axis.
So point (x1, y1) is actually at (0, b)
and the equation becomes:Start withy − y1 = m(x − x1)(x1, y1) is actually (0, b):y − b = m(x − 0)Which is:y − b = mxPut b on other side:y = mx + b
Conclusion
Slope intercept form equations are useful for solving straight line problems, but there are times when you need the point slope form to get an answer. What is that? You may be asking yourself that question. “Where will I need this?” you think. Well, if you’re conquering linear systems, measuring incline of a non-horizontal slope, or figuring out the distance between two points of interest on a line — all important skills to have in math class or on the SAT! If you did algebra in school but forgot what the formulas look like…