How to Solve Slope-Intercept Form – Slope-intercept form is the standard representation of a linear equation using two variables. It may also be called standard form. It is one of the most useful forms for solving algebraic equations, because it can yield insight into the role of any variable in an equation.
Slope-intercept form is probably the most basic form of linear equations. Almost all other forms are variations of the slope-intercept form. Hopefully this post would help you to be able to solve slope intercepts yourself, instead of having to find someone to do them for you.
There are several forms that the equation of a line can take. They may look different, but they all describe the same line–a line can be described by many equations. All (linear) equations describing a particular line, however, are equivalent.
The first of the forms for a linear equation is slope-intercept form. Equations in slope-intercept form look like this:
| y = mx + b |
where m is the slope of the line and b is the y-intercept of the line, or the y-coordinate of the point at which the line crosses the y-axis.
To write an equation in slope-intercept form, given a graph of that equation, pick two points on the line and use them to find the slope. This is the value of m in the equation. Next, find the coordinates of the y-intercept–this should be of the form (0, b). The y– coordinate is the value of b in the equation.
Finally, write the equation, substituting numerical values in for m and b. Check your equation by picking a point on the line (not the y-intercept) and plugging it in to see if it satisfies the equation.
Example 1: Write an equation of the following line in slope-intercept form:
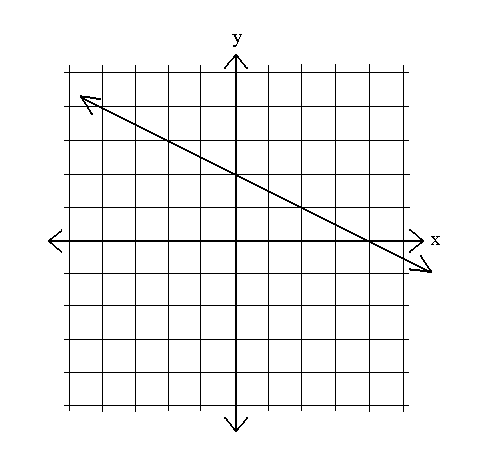
First, pick two points on the line–for example, (2, 1) and (4, 0). Use these points to calculate the slope: m =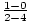 
= 
= – 
.
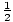Next, find the y-intercept: (0, 2). Thus, b = 2.
Therefore, the equation for this line is y = – 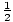x + 2.
Check using the point (4, 0): 0 = – 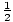(4) + 2 ? Yes.
Example 2: Write an equation of the line with slope m =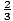 
which crosses the y-axis at (0, – 
).
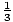y = 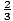x –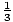
Example 3: Write an equation of the line with y-intercept 3 that is parallel to the line y = 7x – 9.
Since y = 7x – 9 is in slope-intercept form, its slope is 7.
Since parallel lines have the same slope, the slope of the new line will also be 7. m = 7. b = 3.
Thus, the equation of the line is y = 7x + 3.
Example 4: Write an equation of the line with y-intercept 4 that is perpendicular to the line 3y – x = 9.
The slope of 3y – x = 9 is .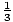
Since the slopes of perpendicular lines are opposite reciprocals, m = – 3. b = 4.
Thus, the equation of the line is y = – 3x + 4.
To summarize how to write a linear equation using the slope-interception form you
- Identify the slope, m. This can be done by calculating the slope between two known points of the line using the slope formula.
- Find the y-intercept. This can be done by substituting the slope and the coordinates of a point (x, y) on the line in the slope-intercept formula and then solve for b.
Once you’ve got both m and b you can just put them in the equation at their respective position.
Table of Contents
Real World Problems
When you have a real world problem, there are two things that you want to look for!
1. Rate: The rate is your slope in the problem. The following are examples of a rate:
- $3 per day
- $2 an hour
- $5 per person
- $6 a minute
This number is always related to the x value.
“Per” is a key word that is often associated with slope or a rate.
2. A Flat Fee: A flat fee is your y-intercept. This value is a constant or fixed amount. It never changes!
Use the chart below to help you organize your information as you analyze each word problem. This will help you when writing equations
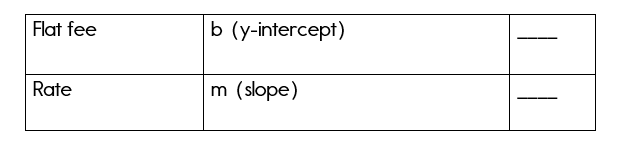
Take a look at the examples below to better clarify how this chart can help you.
Example 3: Writing Equations for Real World Problems
You are visiting Baltimore, MD. A taxi company charges a flat fee of $3.00 plus an additional $0.75 per mile. Write an equation that you could use to find the cost of a taxi ride in Baltimore, MD. Let x represent the number of miles and y represent the total cost.
- How much would a taxi ride for 8 miles cost?
Solution
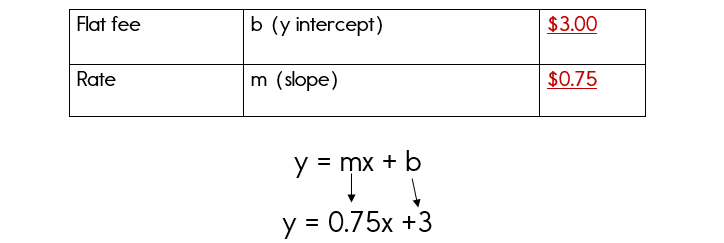
The y-intercept is 3. Since there is a flat fee of $3, this value becomes the y-intercept. It is a constant, a value that never changes.
The slope is 0.75. This is the rate per mile. A rate is also the slope.
Therefore, the equation that represents this problem is y = 0.75x + 3
- How much would a taxi ride for 8 miles cost?
In order to determine this cost, we will need to use our equation and substitute 8 for x.
y = 0.75x + 3
y = 0.75(8) + 3
9 = (0.75)(8) + 3
The cost of an 8 mile taxi ride is $9.
Hopefully you now have the hang of writing equations in slope intercept form.
Remember to always look for the slope and the y-intercept.
Conclusion
We can use a slope-intercept equation to write a linear equation in the standard slope-intercept form, which is a quick way to determine a line graph.