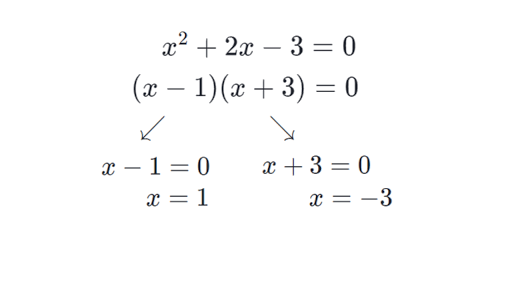How to Solve Quadratic Equations by Factoring – This is the easiest method of solving a quadratic equation as long as the binomial or trinomial is easily factorable. Otherwise, we will need other methods such as completing the square or using the quadratic formula.
A Quadratic Equation in Standard Form
(a, b, and c can have any value, except that a can’t be 0.)
“Factoring” (or “Factorising” in the UK) a Quadratic is:
finding what to multiply to get the Quadratic
It is called “Factoring” because we find the factors (a factor is something we multiply by)
Table of Contents
Example:
Multiplying (x+4) and (x−1) together (called Expanding) gets x2 + 3x − 4 :

So (x+4) and (x−1) are factors of x2 + 3x − 4
Just to be sure, let us check: (x+4)(x−1) = x(x−1) + 4(x−1) = x2 − x + 4x − 4 = x2 + 3x − 4
Yes, (x+4) and (x−1) are definitely factors of x2 + 3x − 4
Did you see that Expanding and Factoring are opposites?

Expanding is usually easy, but Factoring can often be tricky.
It is like trying to find which ingredients
went into a cake to make it so delicious.
It can be hard to figure out!
So let us try an example where we don’t know the factors yet:
Common Factor
First check if there any common factors.
Example: what are the factors of 6x2 − 2x = 0 ?
6 and 2 have a common factor of 2:
2(3x2 − x) = 0
And x2 and x have a common factor of x:
2x(3x − 1) = 0
And we have done it! The factors are 2x and 3x − 1,
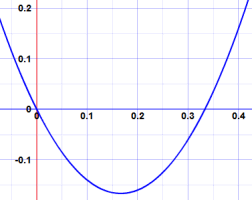
We can now also find the roots (where it equals zero):
- 2x is 0 when x = 0
- 3x − 1 is zero when x = 13
And this is the graph (see how it is zero at x=0 and x=13):
But it is not always that easy …
Guess and Check
Maybe we can guess an answer?
Example: what are the factors of 2x2 + 7x + 3 ?
No common factors.
Let us try to guess an answer, and then check if we are right … we might get lucky!
We could guess (2x+3)(x+1):
(2x+3)(x+1) = 2x2 + 2x + 3x + 3
= 2x2 + 5x + 3 (WRONG)
How about (2x+7)(x−1):
(2x+7)(x−1) = 2x2 − 2x + 7x − 7
= 2x2 + 5x − 7 (WRONG AGAIN)
OK, how about (2x+9)(x−1):
(2x+9)(x−1) = 2x2 − 2x + 9x − 9
= 2x2 + 7x − 9 (WRONG AGAIN)
Oh No! We could be guessing for a long time before we get lucky.
That is not a very good method. So let us try something else.
A Method For Simple Cases
Luckily there is a method that works in simple cases.
With the quadratic equation in this form:

Step 1: Find two numbers that multiply to give ac (in other words a times c), and add to give b.
Example: 2x2 + 7x + 3
ac is 2×3 = 6 and b is 7
So we want two numbers that multiply together to make 6, and add up to 7
In fact 6 and 1 do that (6×1=6, and 6+1=7)
How do we find 6 and 1?
It helps to list the factors of ac=6, and then try adding some to get b=7.
Factors of 6 include 1, 2, 3 and 6.
Aha! 1 and 6 add to 7, and 6×1=6.
Step 2: Rewrite the middle with those numbers:
Rewrite 7x with 6x and 1x:
2x2 + 6x + x + 3
Step 3: Factor the first two and last two terms separately:
The first two terms 2x2 + 6x factor into 2x(x+3)
The last two terms x+3 don’t actually change in this case
So we get:
2x(x+3) + (x+3)
Step 4: If we’ve done this correctly, our two new terms should have a clearly visible common factor.
In this case we can see that (x+3) is common to both terms, so we can go: Start with:2x(x+3) + (x+3) Which is:2x(x+3) + 1(x+3) And so:(2x+1)(x+3)
Done!
Check: (2x+1)(x+3) = 2x2 + 6x + x + 3 = 2x2 + 7x + 3 (Yes)
Much better than guessing!
Let’s see Steps 1 to 4 again, in one go:
| 2x2 + 7x + 3 |
| 2x2 + 6x + x + 3 |
| 2x(x+3) + (x+3) |
| 2x(x+3) + 1(x+3) |
| (2x+1)(x+3) |
OK, let us try another example:
Example: 6x2 + 5x − 6
Step 1: ac is 6×(−6) = −36, and b is 5
List the positive factors of ac = −36: 1, 2, 3, 4, 6, 9, 12, 18, 36
One of the numbers has to be negative to make −36, so by playing with a few different numbers I find that −4 and 9 work nicely:
−4×9 = −36 and −4+9 = 5
Step 2: Rewrite 5x with −4x and 9x:
6x2 − 4x + 9x − 6
Step 3: Factor first two and last two:
2x(3x − 2) + 3(3x − 2)
Step 4: Common Factor is (3x − 2):
(2x+3)(3x − 2)
Check: (2x+3)(3x − 2) = 6x2 − 4x + 9x − 6 = 6x2 + 5x − 6 (Yes)
Finding Those Numbers
The hardest part is finding two numbers that multiply to give ac, and add to give b.
It is partly guesswork, and it helps to list out all the factors.
Here is another example to help you:
Example: ac = −120 and b = 7
What two numbers multiply to −120 and add to 7 ?
The factors of 120 are (plus and minus):
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120
We can try pairs of factors (start near the middle!) and see if they add to 7:
- −10 x 12 = −120, and −10+12 = 2 (no)
- −8 x 15 = −120 and −8+15 = 7 (YES!)
Solve the quadratic equation below using the Factoring Method.
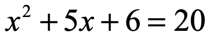
The first thing I realize in this problem is that one side of the equation doesn’t contain zero. I can easily create a zero on the right side by subtracting both sides by 202020.
After doing so, the left side should have a factorable trinomial that is very similar to problem 3.
To factor out this trinomial, think of two numbers when multiplied together gives −14 – 14−14 (constant term) and when added gives +5 + 5+5 (coefficient of xxx-term). By trial and error, the numbers should be −2 – 2−2 and 777. You may verify this correct combination.
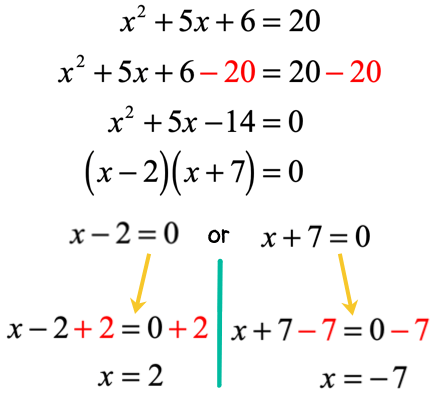
The final answers are x=2x = 2x=2 and x=− 7x = – \,7x=−7.
Example 6: Solve the quadratic equation below using the Factoring Method.
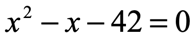
Solution:
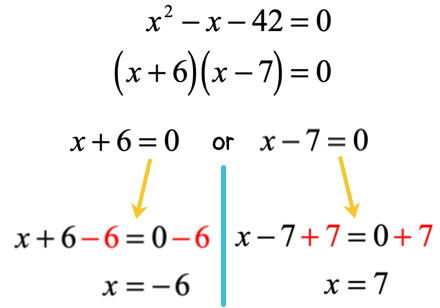
Here we have x=− 6x = – \,6x=−6 and x=7x = 7x=7 as our final answers.
Example: Solve the quadratic equation below using the Factoring Method.
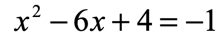
Solution:
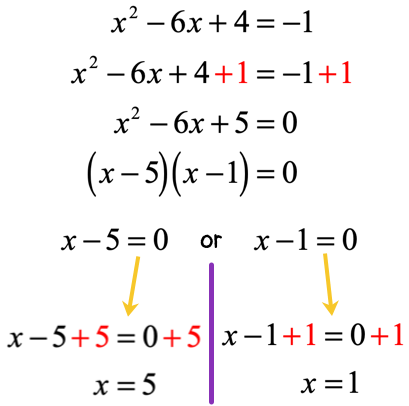
Our final answers are x=5x = 5x=5 and x=1x = 1x=1.