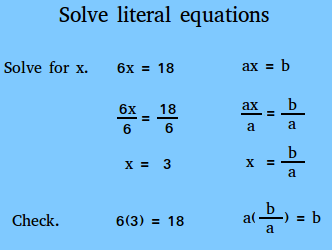How to Solve Literal Equations

How to Solve Literal Equations – Sometimes we are given a formula, such as something from geometry, and we need to solve for some variable other than the “standard” one. For instance, the formula for the perimeter P of a square with sides of length s is P = 4s. We might need to solve this equation for s because we have a lot of squares’ perimeters, and we want to plug those perimeter values into one formula and have that formula (maybe in our graphing calculator) spit out the value for the length of each square’s side. This process of solving a formula for a specified variable is called “solving literal equations”.

One of the dictionary definitions of “literal” is “related to or being comprised of letters”, and variables are sometimes referred to as literals. So “solving literal equations” seems to be another way of saying “taking an equation with lots of letters, and solving for one letter in particular.”

At first glance, these exercises appear to be much worse than our usual solving exercises, but they really aren’t that bad. We pretty much do what we’ve done all along for solving linear equations and other sorts of equation; the only substantial difference is that, due to all the variables, we won’t be able to simplify our work as we go along, nor as much as we’re used to at the end.

Table of Contents

Method 1 :Rearranging Geometric Formulas

Determine which variable you need to isolate. Isolating a variable means getting the variable on one side of an equation by itself. This information should be given to you, or you can figure it out based on what information you know you will be given.
- For example, you might be told to solve the area of a triangle formula for $h$ . Or, you might know that you have the area and base of the triangle, so you need to solve for the height. So, you need to rearrange the formula and isolate the $h$ variable.
Use algebra to solve for the desired variable. Use inverse operations to cancel variables on one side of the equation and move them to the other side. Keep in mind the following inverse operations:
- Multiplication and division.
- Addition and subtraction.
- Squaring and taking a square root.
Keep the equation balanced. Whatever you do to one side of the equation, you must also do to the other side. This ensures that your equation remains true, and in the process you are moving variables from one side to the other as needed.
- For example, to solve the area of a triangle formula () for :
  - Cancel the fraction by multiplying each side by 2:
    $A\times 2=2\times {\frac {1}{2}}bh$
    $2A=bh$
  - Isolate $h$ by dividing each side by $b$ :
    ${\frac {2A}{b}}={\frac {bh}{b}}$
    ${\frac {2A}{b}}=h$
- Rearrange the formula, if desired: $h={\frac {2A}{b}}$

Method 2: Rearranging Equations of Lines

1Remember the slope-intercept form for the equation of a line. The slope-intercept form is $y=mx+b$ , where $y$ equals the y-coordinate of a point on the line, $x$ equals the x-coordinate of that same point, $m$ equals the slope of the line, and $b$ equals the y-intercept.
Remember the standard form of a line. The standard form is $Ax+By=C$ , where $x$ and $y$ are the coordinates of a point on the line, $A$ is a positive integer, and $B$ and $C$ are integers.
Use algebra to isolate the appropriate variable. Use inverse operations to move variables from one side of the equation to the other side. Remember to keep the equation balanced, which means that whatever you do to one side of the equation, you must also do to the other side.
- For example, you might have the equation of a line . This is in standard form. If you need to find the y-intercept of the line, you need to rearrange the formula to slope-intercept form by isolating the variable:
  - Subtract $3x$ from both sides of the equation:
    $3x+2y-3x=4-3x$
    $2y=4-3x$ .
  - Divide both sides by $2$ :
    ${\frac {2y}{2}}={\frac {4-3x}{2}}$
    $y={\frac {4-3x}{2}}$
Reorder the variables and constants, if necessary. If you are changing an equation to slope-intercept or standard form, rearrange the variables, coefficients, and constants so that they follow the correct formula.
- For example, to change $y={\frac {4-3x}{2}}$ to the correct slope-intercept formula, you need to switch the order of the number in the numerator, then simplify:
  $y={\frac {-3x+4}{2}}$
  $y={\frac {-3}{2}}x+2$
  Now, since the formula is in proper slope-intercept form, it is easy to identify the y-intercept as 2.

Method 3: Solving Sample Problems

Solve this equation for b. .
- Factor out the $b$ : $R=b(5d-6a)$ .
- Isolate the $b$ by dividing each side by the expression in parentheses:
  ${\frac {R}{5d-6a}}={\frac {b(5d-6a)}{5d-6a}}$
  ${\frac {R}{5d-6a}}=b$
Solve the circumference of a circle formula for the radius. The formula is
- Understand what each variable stands for. In this formula, $C$ is the circumference, and $r$ is the radius. So you need to isolate the $r$ to solve for the radius.
- Isolate the $r$ by dividing both sides of the equation by $2\pi$ :
  ${\frac {C}{2\pi }}={\frac {2\pi {r}}{2\pi }}$
  ${\frac {C}{2\pi }}=r$
- If desired, reverse the order of the equation for standard form: $r={\frac {C}{2\pi }}$ .
Rewrite this equation of a line in standard form.
- Recall that standard form is $Ax+By=C$ .
- Cancel the fraction by multiplying each side of the equation by 2:
  $2y=2({\frac {1}{2}}x+5)$
  $2y=x+10$
- Subtract $x$ from both sides of the equation:
  $2y-x=x+10-x$
  $2y-x=10$
- Rearrange the $y$ and $x$ variables so that they are in the standard form: $-x+2y=10$ .
- Multiply both sides by $-1$ , since $A$ should be a positive integer for standard form:
  $-1(-x+2y)=-1(10)$
  $x-2y=-10$

An Example of One-Step Literal Equation

Example 1: Solve for s in the literal equation P = 4s.

Remember this formula? This is the perimeter of a square where P stands for perimeter and s stands for the measure of one side of a square. Thus, to get the perimeter of a square we have P = s+s+s+s = 4s.

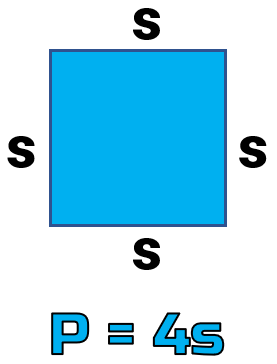
a blue square with a side measure of "s" which implies that its perimeter is four times the length of one side.

To solve for s, we need to get rid of the coefficient 4 which is multiplying s. The inverse of multiplication is division, and that’s why we should divide both sides by 4!

We can isolate variable s on the right side.

P is equal to the product of 4 and s. In short, we have P=4s.

Divide both sides by 4.

the quotient of P and 4 is equal to the quotient of 4s and 4. We can write this as P/4=(4s)/4.

Simplify. Now the variable \color{red}\Large{s}s is alone on the right side of the equation. We are done!

P divided by 4 equals s. We write this in an equation as P/4=s.

Examples of Two-Step Literal Equations

Example 2: Solve for L in the literal equation P = 2L + 2W.

Well, this is the formula to get the perimeter of a rectangle where: P = perimeter, L = length, and W = width. It is possible to isolate the variable L on the right side, however, why not flip the equation around so we can keep the variable L alone on the left? Sounds like a plan!

Don’t be intimidated by how it looks. Just focus on the things you want to do, that is to solve for L and the rest of the steps will follow.

We want L solved, right?

P is equal to the sum of the products of 2 and L, and 2 and W. It can be written as P=2L+2W.

Flip around the equation to isolate the variable on the left side.

Subtract both sides by 2W.

Simplify.

Divide both sides by 2.

Simplify, now L stands alone – solved!

Example 3: Solve for x in the literal equation below.

m is equal to the ratio of the difference of x and y, and 3. we can write this as m=(x-y)/3.

What makes this literal equation interesting is that we are going to isolate a variable that is part of the numerator of a fraction. I’m not sure if you remember that whenever you see something like this, try to get rid of the denominator first. This makes the entire solving process a lot simpler.

Since that denominator 3 is dividing the expression “x − y”, the opposite operation that can undo it is multiplication. It makes sense to multiply both sides by 3 first, then add by “y” to keep the x by itself. Not too bad, right?https://a56a25edd6415bb66c01ca6077c56b74.safeframe.googlesyndication.com/safeframe/1-0-38/html/container.html

Okay, we want to solve for x. Let’s isolate it on the right side.

Start by multiplying both sides by 3 which is the denominator of the fraction.

multiply 3 on both sides of the equation m=(x-y)/3.

Simplify. That’s good, the denominator is now gone.

Add both sides by y. That’s the only way to eliminate that − y on the right side.

Simplify, x is now happily by itself. Done!

Examples of Multi-Step Literal Equations

Example 4: Solve for C in the literal equation below.

this is the formula to convert Celsius to Fahrenheit

This is the formula used to convert the measure of temperature in the Celsius unit to the Fahrenheit scale. Notice that to find the value of F (Fahrenheit), we need to plug in some value of C (Celsius).

However, can we also use the given formula to find Celsius whenever the value for Fahrenheit is given?

Absolutely yes!

This is a literal equation after all so it is possible to express C in terms of F. That’s what we’re going to do now…

All eyes on C. The goal is to isolate it.

We’ll get rid of that 32 on the right by subtracting both sides by 32.

This looks cleaner after simplification.

Next, multiply both sides by 5 to cancel out that denominator 5 under 9C.

multiply 5 to both sides of the equation F-32=(9C)/5.

We’re getting there! I suggest not to distribute that 5 into (F − 32).

One more step, divide both sides by 9 to finally isolate the variable on the right.

divide both sides by 9 to get the formula to determine Celsius value when a Fahrenheit temperature is given

That’s it! We have solved for C.

Example 5: Solve for h in the literal equation 3h + g = 5h − hg.

This is really interesting! Some of you might think that it is impossible to isolate the variable h since it is found pretty much in three places – one h on the left and two on the right. Well, don’t give up yet! Let me show you a little “secret”.

Use the factoring method to pick that variable h out of the group. But before you could factor h out, make sure that you move all the h’s on one side of the equation.

Since we have two terms of h’s on the right side, we might as well move the term 3h on the left to the other side.