How to Solve X Intercept

How to Solve X Intercept – The x-intercepts are points where the graph of a function or an equation crosses or “touches” the x-axis of the Cartesian Plane. You may think of this as a point with y-value of zero.

To find the x-intercepts of an equation, let y = 0y=0 then solve for xx.
In a point notation, it is written as \left( {x,0} \right)(x,0).

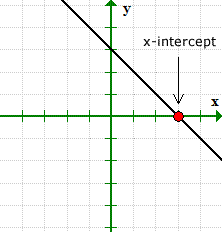
x-intercept of a Linear Function or a Straight Line

the x-intercept of a line as shown on a graph

x-intercepts of a Quadratic Function or Parabola

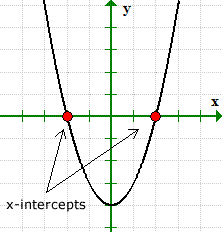
Table of Contents

The Y-Intercepts

The y-intercepts are points where the graph of a function or an equation crosses or “touches” the y-axis of the Cartesian Plane. You may think of this as a point with x-value of zero.https://imasdk.googleapis.com/js/core/bridge3.491.0_en.html#goog_5878300921 second of 30 secondsVolume 0%

To find the y-intercepts of an equation, let x = 0x=0 then solve for yy.
In a point notation, it is written as \left( {0,y} \right)(0,y).

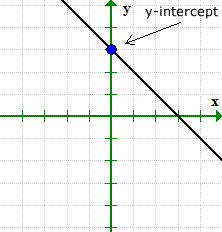
y-intercept of a Linear Function or a Straight Line

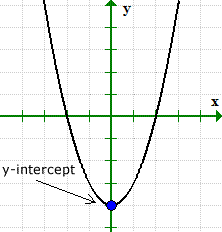
y-intercept of a line or linear function on a graph

y-intercept of a Quadratic Function or Parabola

y-intercept of a quadratic function illustrated on xy-axis

Examples of How to Find the x and y-intercepts of a Line, Parabola, and Circle

Example 1: From the graph, describe the x and y-intercepts using point notation.

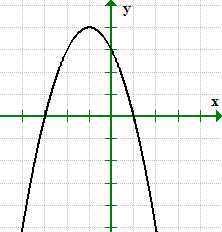
the graph of a quadratic function with x-intercepts of 1 and 3, and y-intercept of 3.

The graph crosses the x-axis at x= 1x=1 and x= 3x=3, therefore, we can write the x-intercepts as points (1,0) and (–3, 0).

Similarly, the graph crosses the y-axis at y=3y=3. Its y-intercept can be written as the point (0,3).

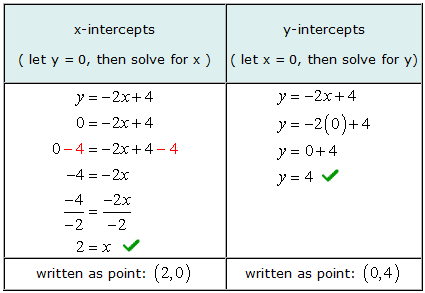
Example 2: Find the x and y-intercepts of the line y = –2x + 4.

To find the x-intercepts algebraically, we let y=0y=0 in the equation and then solve for values of xx. In the same manner, to find for y-intercepts algebraically, we let x=0x=0 in the equation and then solve for yy.

x-intercept at (2,0), and y-intercept at (0,4)

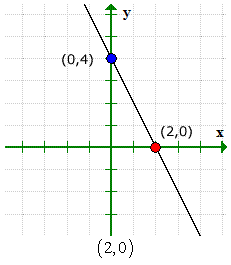
Here’s the graph to verify that our answers are correct.

a line with an y-intercept at (0,4) and x-intercept at (2,0)

Example 3: Find the x and y-intercepts of the quadratic equation y = x² − 2x − 3.

The graph of this quadratic equation is a parabola. We expect it to have a “U” shape where it would either open up or down.

To solve for the x-intercept of this problem, you will factor a simple trinomial. Then you set each binomial factor equal to zero and solve for x.

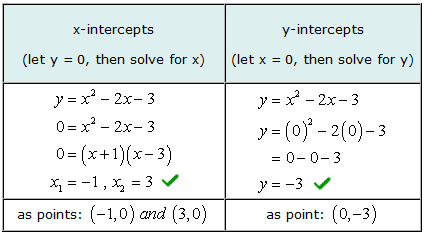
x-intercepts at (-1,0) and (3,0); y-intercept at (0,-3)

Our solved values for both x and y-intercepts match with the graphical solution.

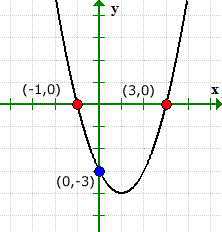
the graph of a quadratic function with x-intercepts at (-1,0) and (3,0), and y-intercept at (0,-3)

Example 4: Find the x and y-intercepts of the quadratic equation y = 3x² + 1.

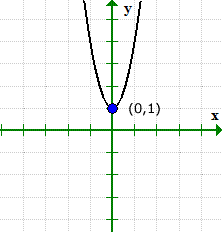
This is an example where the graph of the equation has a y-intercept but without an x-intercept.

Let’s find the y-intercept first because it’s extremely easy! Plug in x = 0 then solve for y.

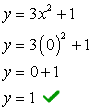
Now for the x-intercept. Plug in y = 0, and solve for x.

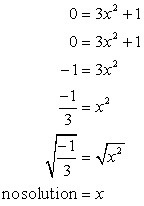
The square root of a negative number is imaginary. This suggests that this equation does not have an x-intercept!

The graph can verify what’s going on. Notice that the graph crossed the y-axis at (0,1), but never did with the x-axis.

the graph of y=3x^2+1 doesn't cross or touch the x-axis

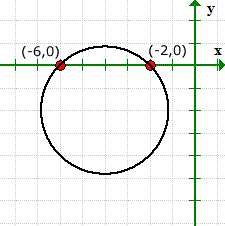
Example 5: Find the x and y intercepts of the circle (x + 4)² + (y + 2)² = 8.

This is a good example to illustrate that it is possible for the graph of an equation to have x-intercepts but without y-intercepts.

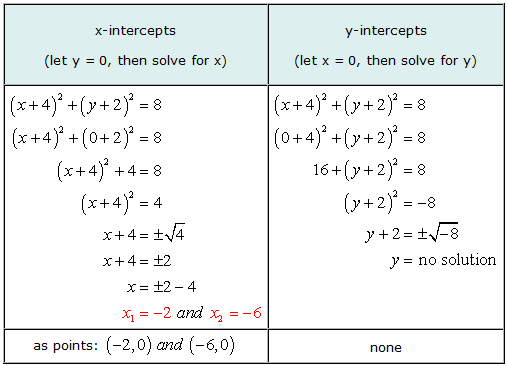
the x-intercepts of a circle are (-2,0) and (-6,0)

When solving for y, we arrived at the situation of trying to get the square root of a negative number. The answer is imaginary, thus, no solution. That means the equation doesn’t have any y-intercepts.

The graph verifies that we are right for the values of our x-intercepts, and it has no y-intercepts.

a circle with x-intercepts at (-6,0) and (-2,0)

How to Find the X Intercept in Three Methods

Method 1 of 3:Using a Graph of a Line

Identify the x-axis. A coordinate graph has a y-axis and an x-axis. The x-axis is the horizontal line (the line that goes from left-to-right). The y-axis is the vertical line (the line that goes up and down).It is important to look at the x-axis when locating the x-intercept.
Find the point where the line crosses the x-axis. The x-intercept is this point. If you are asked to find the x-intercept based on the graph, the point will likely be exact (for example, at point 4). Usually, however, you will have to estimate using this method (for example, the point is somewhere between 4 and 5).
Write the ordered pair for the x-intercept. An ordered pair is written in the form and gives you the coordinates for the point on the line. The first number of the pair is the point where the line crosses the x-axis (the x-intercept). The second number for will always be 0, since a point on the x-axis will never have a value for y.
- For example, if a line crosses the x-axis at point 4, the ordered pair for the x-intercept is $(4,0)$ .

Method 2: Using the Equation of the Line

Determine that the equation of the line is in standard form. The standard form of a linear equation is .^[5]In this form, , , and are integers, and and are the coordinates of a point on the line.
- For example, you might be given the equation $2x+3y=6$ .
Plug in 0 for y. The x-intercept is the point on the line where the line crosses the x-axis. At this point, the value for will be 0. So, in order to find the x-intercept, you need to set the to 0 and solve for .
- For example, if you substitute 0 for $y$ , your equation will look like this: $2x+3(0)=6$ , which simplifies to $2x=6$ .
Solve for x. To do this, you need to isolate the x variable by dividing both sides of the equation by the coefficient. This will give you the value of when , which is the x-intercept.^[7]
- For example:
  $2x=6$
  ${\frac {2x}{2}}={\frac {6}{2}}$
  $x=3$
Write the ordered pair. Remember that an ordered pair is written in the form . For the x-intercept, the value of will be the value you calculated previously, and the value will be 0, since always equals 0 at the x-intercept.
- For example, for the line $2x+3y=6$ , the x-intercept is at the point $(3,0)$ .Advertisement

Method 3: Using the Quadratic Formula

Determine that the equation of the line is a quadratic equation. A quadratic equation is an equation that takes the form .A quadratic equation has two solutions, which means a line written in this form is a parabola and will have two x-intercepts.
- For example, the equation $x^{{2}}+3x-10=0$ is a quadratic equation, so this line will have two x-intercepts.
Set up the quadratic formula. The formula is $x={\frac {-b\pm {\sqrt {b^{{2}}-4ac}}}{2a}}$ , where $a$ equals the coefficient of the second-degree term ( $x^{{2}}$ ), $b$ equals the coefficient of the first-degree term ( $x$ ), and $c$ equals the constant.
Plug all of the values into the quadratic formula. Make sure you substitute the correct values for each variable from the equation of the line.
- For example, if the equation of your line is $x^{{2}}+3x-10=0$ , your quadratic formula will look like this: $x={\frac {-3\pm {\sqrt {3^{{2}}-4(1)(-10)}}}{2(1)}}$ .
Simplify the equation. To do this, first complete all of the multiplication. Make sure you pay close attention to all positive and negative signs.
- For example:
  $x={\frac {-3\pm {\sqrt {3^{{2}}-4(-10)}}}{2(1)}}$
  $x={\frac {-3\pm {\sqrt {3^{{2}}+40}}}{2}}$
Calculate the exponent. Square the term. Then, add this number to the other number under the square root sign.
- For example:
  $x={\frac {-3\pm {\sqrt {3^{{2}}+40}}}{2}}$
  $x={\frac {-3\pm {\sqrt {9+40}}}{2}}$
  $x={\frac {-3\pm {\sqrt {49}}}{2}}$
Solve for the addition formula. Since the quadratic formula has a , you will solve once by adding, and once by subtracting. Solving by adding will give you your first value.
- For example:
  $x={\frac {-3+{\sqrt {49}}}{2}}$
  $x={\frac {-3+7}{2}}$
  $x={\frac {4}{2}}$
  $x=2$
Solve for the subtraction formula. This will give you the second value for {\displaystyle x}. First calculate the square root, then find the difference in the numerator. Finally, divide by 2.
- For example:
  $x={\frac {-3-{\sqrt {49}}}{2}}$
  $x={\frac {-3-7}{2}}$
  $x={\frac {-10}{2}}$
  $x=-5$
Find the ordered pairs for the x-intercept. Remember that an ordered pair gives the x-coordinate first, then the y-coordinate. The values will be the values you calculated using the quadratic formula. The value will be 0, since at the x-intercept, always equals 0.
- For example, for the line $x^{{2}}+3x-10=0$ , the x-intercepts are at points $(2,0)$ and $(-5,0)$ .

Conclusion

In algebra, 2-dimensional coordinate graphs have a horizontal axis, or x-axis, and a vertical axis, or y-axis. The places where lines representing a range of values cross these axes are called intercepts. The y-intercept is the place where the line crosses the y-axis and the x-intercept where the line crosses the x-axis. For simple problems, it is easy to find the x-intercept by looking at a graph.

0 0 votes

Article Rating